11. Cone volume
The volume of a cone
The volume of a circular cone cannot be calculated by filling it with pieces that coincide with its base. Instead, the volume of a circular cone is obtained by filling it with uniformly shaped pieces that decrease in size as you go towards the tip of the cone. Since there is a relationship between the uniform pieces, we can assume that the volume of the cone is obtained as follows:
[[$$ \text{cone volume} = \text{some ratio} · \text{the volume of the corresponding cylinder} $$]]
Regardless of the shape of the base of the cone, its volume is always calculated in the same way. The shape of the base should be taken into account in the formula for its surface area.
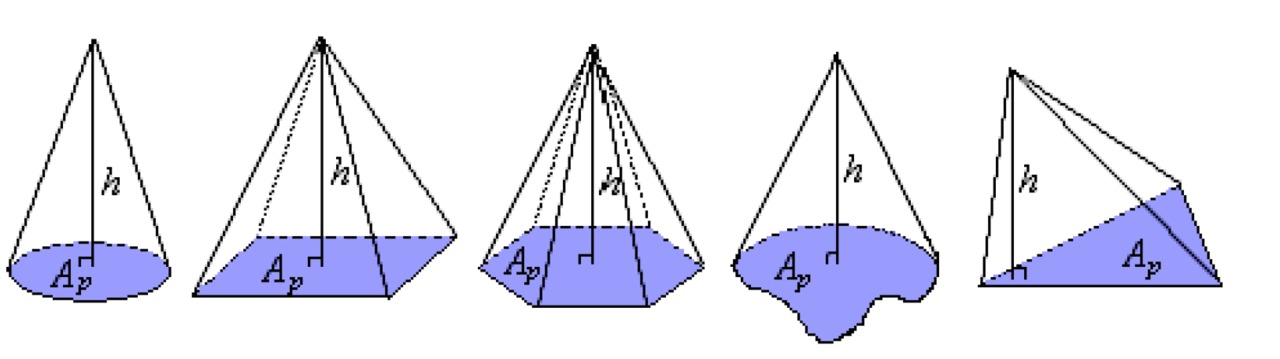
Cone volume
The volume of a cone is [[$ \displaystyle\frac {1} {3} $]] the volume of a cylinder whose base area [[$ A_p $]] and height [[$ h $]] are the same as those of the cone.[[$$ V = \displaystyle\frac {1} {3} A_p h $$]]
Example 1
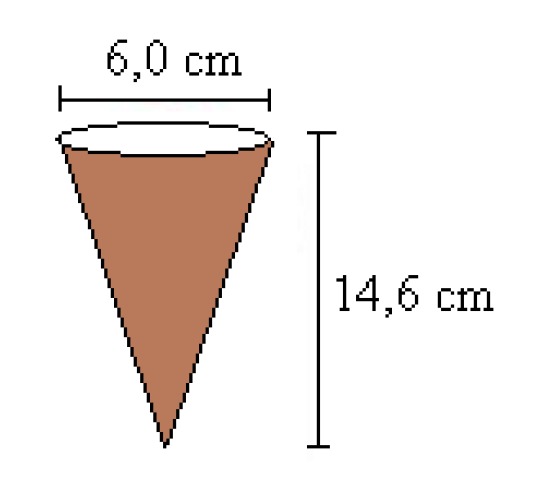
Calculate the volume of the ice cream cone.
The ice cream cone has the shape of a circular cone, the base area of which can be calculated from the radius [[$ r $]] as follows: [[$ A_p = \pi r^2 $]]. The formula for calculating the volume of the cone thus takes the form
Answer: The volume of the cone is approximately [[$ 1.4 $]] dl.
Example 2

The Pyramid of Cheops was originally [[$ 147 $]] m high and had a bottom edge of [[$ 230 $]] m. Calculate the volume of the pyramid.
The pyramid is a cone, and its volume can be obtained according to the same calculation rules as those of all other kinds of cones. The base of a pyramid consists of a square whose area is obtained from the edge of the square [[$ s $]] as follows [[$ A_p = s^2 $]]. Therefore, the volume of the pyramid is
[[$ \begin{align*}
V &= \displaystyle\frac {1} {3} A_p h\\
&= \displaystyle\frac {1} {3} s^2 h \\
&= \displaystyle\frac {1} {3} \cdot (230 \text {m})^2 \cdot 147 \text {m} \\
&≈ 2,6 \cdot 10^6 \text {m}^3
\end{align*} $]]
Answer: The volume of the Pyramid of Cheops was originally [[$ 2.6 \cdot 10^6 \text {m}^3 $]].
Exercises
Basic exercises
Applied exercises
Challenging exercises
2/11. Submission folder
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.