9. Units of volume
Units of volume
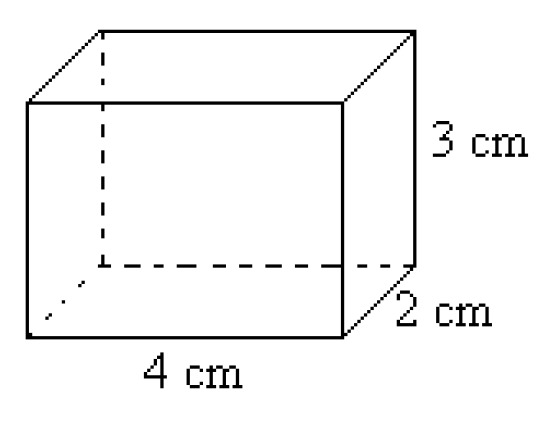
Consider a right polyhedron with the length of [[$ 4 $]] cm, width of [[$ 2 $]] cm and height of [[$ 3 $]] cm.
The volume of a right polyhedron is determined by examining how many times a selected unit of measurement fits inside the polyhedron. Since the dimensions of a rectangle are given in centimeters, it is natural to choose a cube that is one centimeter long on all sides as the unit of measurement.
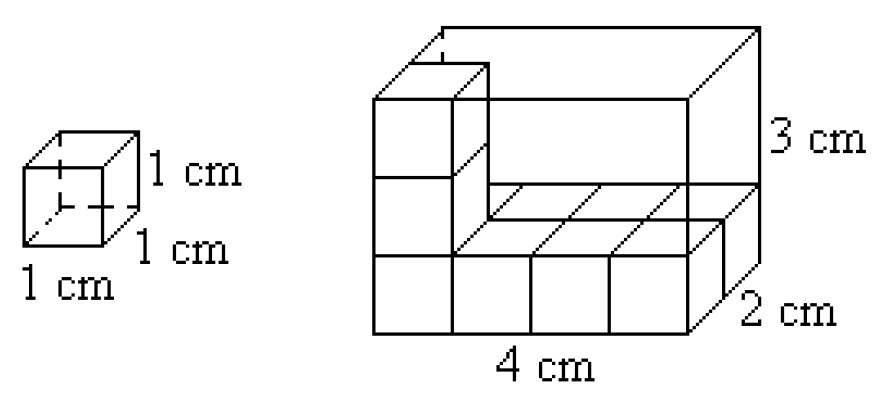
[[$ 4 \cdot 2 = 8 $]] of such small cubes fit on the bottom of a right polyhedron, and three such layers are formed. This means that a total of [[$ 3\cdot 8 = 24 $]] such cubes can fit inside the polyhedron. Thus, the volume of a right polyhedron is obtained by calculating the product of its base area and height.
If the lengths of the edges of a polyhedron are [[$ a $]], [[$ b $]] and [[$ c $]], its volume is
[[$$ V = abc $$]]
The unit of volume is thus [[[$ V $]]] = [[[$ a $]]][[[$ b $]]][[[$ c $]]] = cm · cm · cm = cm[[$ ^3 $]].
Units of volume
Volume units are the third powers or cubes of length units. The length dimension ratio is [[$ 10 $]], which means that the volume dimension ratio must be [[$ 10\cdot10\cdot10= 1,000 $]]. Thus, when moving to the next unit of measurement, the position of the comma must be moved by three steps.
| unit | name | in base units |
|---|---|---|
| mm[[$ ^3 $]] | cubic millimeter | [[$ 0,000000001 $]] m[[$ ^3 $]] |
| cm[[$ ^3 $]] | cubic centimeter | [[$ 0,000001 $]] m[[$ ^3 $]] |
| dm[[$ ^3 $]] | cubic decimeter | [[$ 0,001 $]] m[[$ ^3 $]] |
| m[[$ ^3 $]] | cubic meter | [[$ 1 $]] m[[$ ^3 $]] |
Litres
Liter units are used to express volumes of liquid substances. The ratio of consecutive liter units is [[$ 10 $]]. Therefore, when moving to the next liter unit, only one step needs to be moved.
| symbol | name | in base units |
|---|---|---|
| ml | milliliter | [[$ 0,001 \; \text {l} $]] |
| cl | centiliter | [[$ 0,001 \;\text {l} $]] |
| dl | deciliter | [[$ 0,01 \;\text {l} $]] |
| l | liter | [[$ 1 \;\text {l} $]] |
Volume and litre units have corresponding units, for example [[$ 1 \;\text {liter} = 1 \;\text {dm}^3 $]].
Example 1
Convert [[$ 540 000 000 $]] mm[[$ ^3 $]] into cubic meters.
[[$ 540\;000\;000 \;\text {mm}^3 = 540\;000 \;\text {cm}^3 \\ 540\;000 \;\text {cm}^3 = 540 \;\text {dm}^3 \\ 540 \;\text {dm}^3 = 0,54 \;\text {m}^3 \\ $]]Answer: [[$ 540\;000\;000 \;\text{mm}^3 $]] is equal to[[$ 0,54 \;\text m^3 $]].
Example 2
Convert [[$ 0,55 $]] litres into cubic centimeters.
[[$ 0,55 \;\text{l} = 0,55 \;\text{dm}^3 = 550 \;\text{cm}^3 $]]
Answer: [[$ 0,55 $]] litres is [[$ 550 \;\text{cm}^3 $]].
Exercises
Basic exercises
Applied exercises
Challenging exercises
2/09. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.