2. The quotient of powers with the same base and the zero exponent
Exercises
The quotient of powers with same base
The quotient [[$ \dfrac{4^5}{4^2} $]] is called a quotient of powers with the same base.
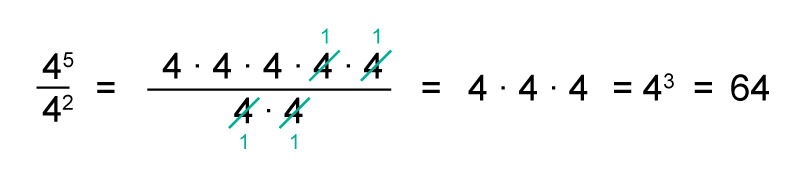
b) [[$ \dfrac{(-4)^7}{(-4)^5} = (-4)^{7-5} = (-4)^2 = 16 $]]
c) [[$ \dfrac{y^7}{y^3} = y^{7-3} = y^4 $]]
d) [[$ \dfrac{a^3 \cdot a^4 \cdot a^6}{a^2 \cdot a^5} = \dfrac{a^{3+4+6}}{a^{2+5}} = \dfrac{a^{13}}{a^7} = a^{13-7} = a^6 $]]
b) [[$ \dfrac{-3^8}{3^5} = -3^{8-5} = -3^3 = -27 $]]
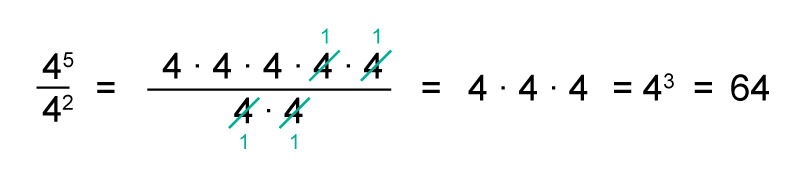
The quotient of powers with the same base
Powers with same base are divided so that the exponent of the denominator is subtracted from the exponent of the numerator. The base number stays the same.
[[$ \dfrac{a^m}{a^n} = a^{m-n}$]]
Example 1
Simplify the powers.
a) [[$ \dfrac{2^6}{2^3} = 2^{6-3} = 2^3 = 8 $]]b) [[$ \dfrac{(-4)^7}{(-4)^5} = (-4)^{7-5} = (-4)^2 = 16 $]]
c) [[$ \dfrac{y^7}{y^3} = y^{7-3} = y^4 $]]
d) [[$ \dfrac{a^3 \cdot a^4 \cdot a^6}{a^2 \cdot a^5} = \dfrac{a^{3+4+6}}{a^{2+5}} = \dfrac{a^{13}}{a^7} = a^{13-7} = a^6 $]]
There are often other factors involved in the quotient of powers with the same base, so you should be careful with the base number.
Example 2
Simplify the powers.
a) [[$ \dfrac{3x^4}{x} = 3x^{4-1} = 3x^3 $]]b) [[$ \dfrac{-3^8}{3^5} = -3^{8-5} = -3^3 = -27 $]]
| c) [[$ \dfrac{6a^4b^2}{3ab} = \dfrac{6}{3}a^{4-1}b^{2-1} = 2a^3b^1 = 2a^3b $]] | Divide the numbers and combine powers with same base. |
The zero exponent
Next, let’s look at the division [[$ \dfrac{4^3}{4^3} $]] in two different ways. Let's simplify by the quotient of equal powers and by reducing.
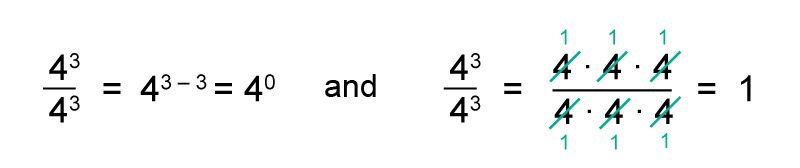
Since both actions are allowed, the results must be equal. In other words, [[$ 4^0 = 1 $]].
b) [[$ -45^0 = -1 $]]
c) [[$ 0^0 $]] cannot be calculated
d) [[$ \dfrac{a^3 \cdot a^9}{a^{12}} = \dfrac{a^{3+9}}{a^{12}} = \dfrac{a^{12}}{a^{12}} = a^{12-12} =a^0 = 1 $]]
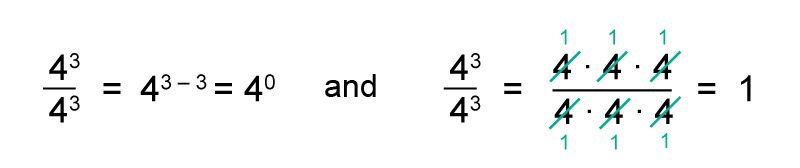
Since both actions are allowed, the results must be equal. In other words, [[$ 4^0 = 1 $]].
Zero as an exponent
If there is a zero as an exponent, the value of the power is always 1. The base number can never be zero.
[[$ a^0 = 1 \text{, kun } a \neq 0. $]]
Example 3
Simplify the powers.
a) [[$ 99^0 = 1 $]]b) [[$ -45^0 = -1 $]]
c) [[$ 0^0 $]] cannot be calculated
d) [[$ \dfrac{a^3 \cdot a^9}{a^{12}} = \dfrac{a^{3+9}}{a^{12}} = \dfrac{a^{12}}{a^{12}} = a^{12-12} =a^0 = 1 $]]