A triangle is a polygon that has three angles. Triangles can be named based on either their angles or their sides.

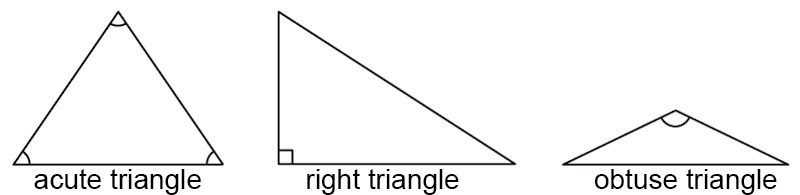
Naming a triangle by its angles

In an acute triangle, all angles are acute, i.e. less than 90°.
A right triangle has one right angle, i.e. one of the angles is 90°.
An obtuse triangle has one obtuse angle, i.e. one of the angles is greater than 90°.

Naming a triangle by its sides

In an equilateral triangle, all the sides are of an equal length.
An isosceles triangle has at least two sides of equal length.

The base angles of an isosceles triangle are always equal. All angles of an equilateral triangle are equal.

The altitude of a triangle is drawn from its apex to the opposite side of the triangle so that it is perpendicular to that side.

The side that is bisected by the triangle's altitude is called the base of the triangle.

The easiest way to draw the altitude of a triangle is with a drawing triangle.

Three kinds of altitudes can be drawn for each triangle. The altitude can either be one of the sides of the triangle, located inside the triangle, or found outside the triangle. If it is not possible to draw a perpendicular from the vertex to the selected base, an extension must be drawn for the base. Usually, the altitude of a triangle is marked by the letter h.

The sum of a triangle's angles

The total sum of the angles of a triangle is always 180°.

Examples

Example 1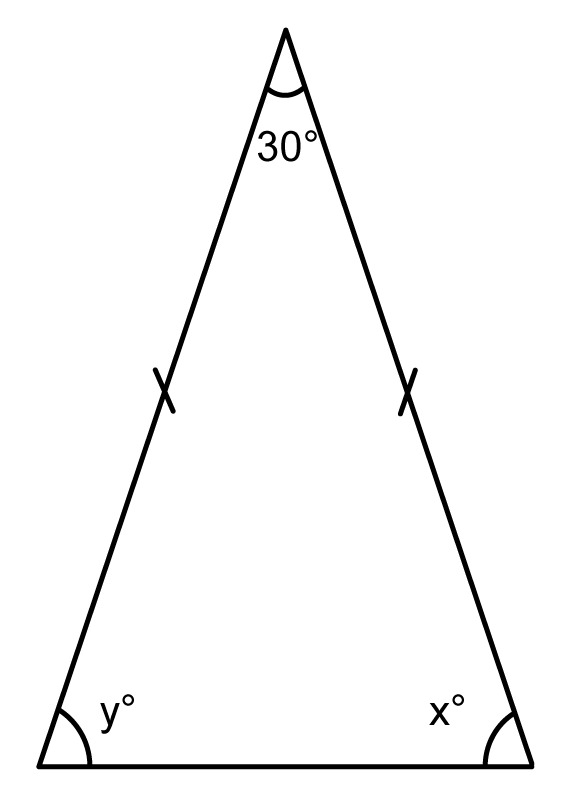

Deduce the magnitudes of angles x and y.

The sum of a triangle's angles is always [[$180°$]], so the sum of the angles x and y is [[$180° - 30° = 150° $]].

Since the triangle is an isosceles triangle , the base angles x and y must be equal. Therefore, the magnitudes of angles x and y are [[$ \dfrac{150°}{2} = 75°$]]

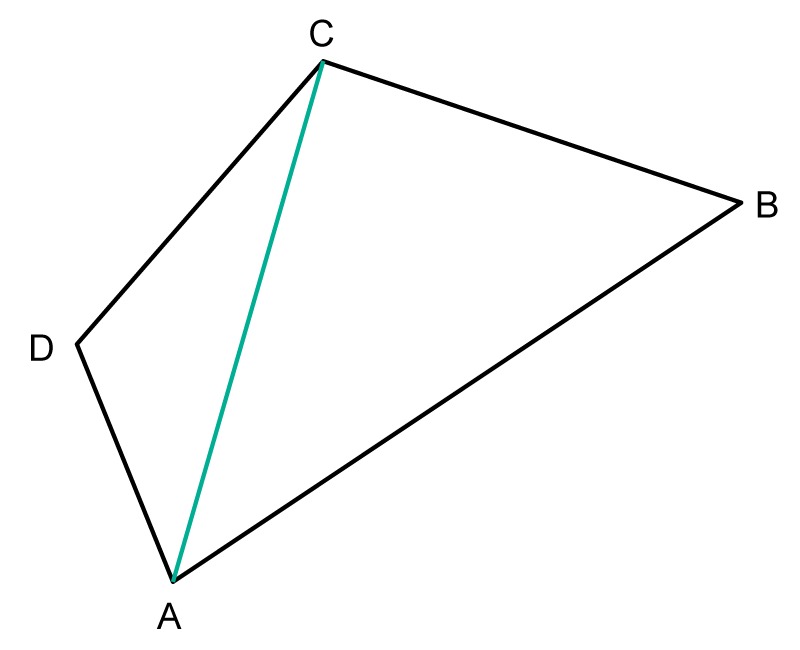
Example 2

Calculate the sum of the angles of the quadrilateral ABCD.

The quadrilateral ABCD can be divided into two triangles, ABC and ACD.

Since the sum of a triangle's angles is [[$180°$]], the sum of the angles of a quadrilateral is [[$ 2 \cdot 180° = 360°$]]. This is true for all quadrilaterals.

The sum of a quadrilateral's angles

The total sum of the angles of a quadrilateral is always 360°.

The sum of the angles of other polygons can be calculated by dividing the polygon into triangles. By doing so, the fact that the sum of a triangle's angles is always [[$180°$]] can be used to calculate the sum of the polygon's angles.