14. Objects and planar intersections
Objects and planar intersections
The Pythagorean theorem in space
The square of the space diagonal of a right triangle is equal to the sum of the squares of its edges.
[[$$ d^2 = a^2 + b^2 + c^2 $$]]
Example 1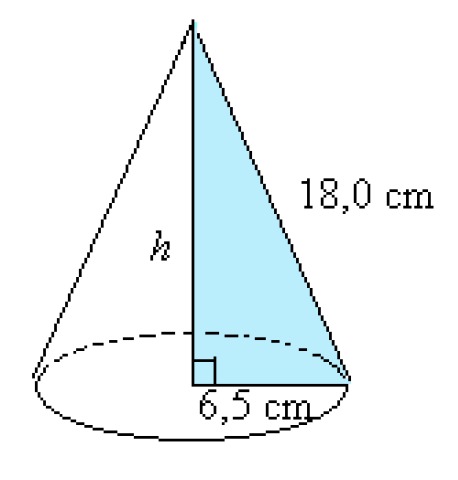
Calculate the volume of a circular cone, when it is known that its side segment is [[$ 18.0 $]] cm long and the radius of the bottom circle is [[$ 6,5 $]] cm.
Solution:
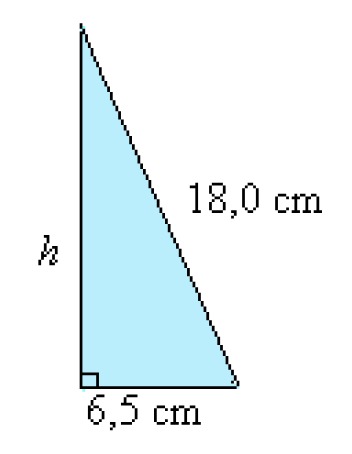
First, the height of the cone is determined with the Pythagorean theorem.
[[$ \begin{align*} h^2 + (6,5 \;\text{cm})^2 &= (18,0\;\text{cm})^2 \\ h^2 &= (18,0\;\text{cm})^2 - (6,5 \;\text{cm})^2 \\ h^2 &= 281,75 \;\text{cm}^2 \\ h &= \sqrt {281,75 \;\text{cm}^2} \\ h &≈ 16,7854 \;\text{cm} \\ \end{align*} $]]
The volume can then be calculated using a the calculation formula for the volume of a circular cone.
[[$ \begin{align*}
V &= \displaystyle\frac \pi r^2 h \\
&= \displaystyle\frac {1} {3} \pi \cdot (6,5 \;\text {cm})^2 \cdot 16,7854 \;\text {cm} \\
&≈ 740 \;\text {cm}^3 \\
\end{align*} $]]
Answer: The volume of the circular cone is [[$ 740 \;\text {cm} $]].
Example 2
Calculate the area of the plate inside the rectangular box.
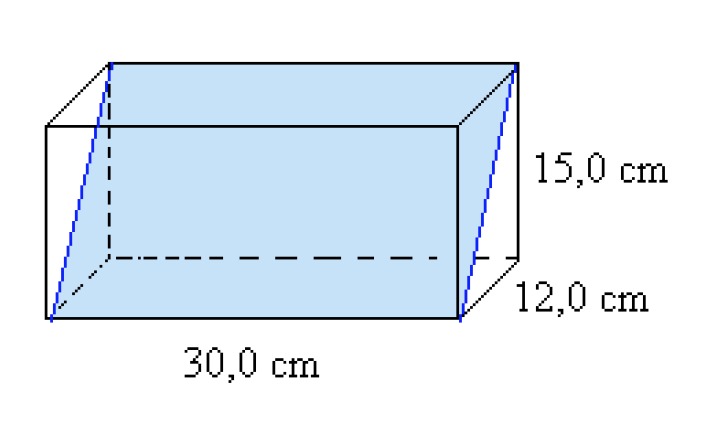
Solution:
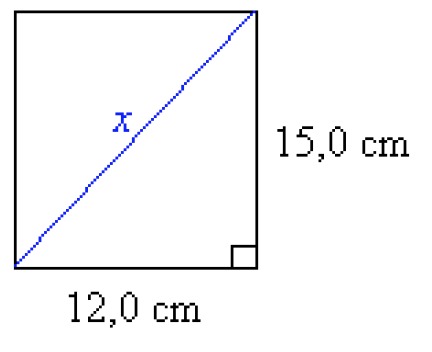
The width of the plate is seen directly from the figure. It is [[$ 30,0 $]] cm. To solve the height of the plate, a picture is drawn from the end of the triangle, on the basis of which the following equation can be written:
[[$ \begin{align*}
x^2 &= (12,0 \;\text{cm})^2 + (15,0 \;\text{cm})^2 \\
x^2 &= 369 \;\text{cm}^2 \\
x &≈ 19,2094 \;\text {cm} \\
\end{align*} $]]
This means that the surface area of the plate is:
[[$ A = 30,0 \;\text{cm} \cdot 19,2094 \;\text{cm} ≈ 576 \,\text{cm}^2 $]].
Answer: The surface area of plate is [[$ 576 \;\text{cm}^2 $]].
Exercises
Basic exercises
Applied exercises
Challenging exercises
2/14. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.