Avaruuskappaleet
Avaruuskappaleet
Kurssissa käsitellään seuraavia avaruuskappaleita:
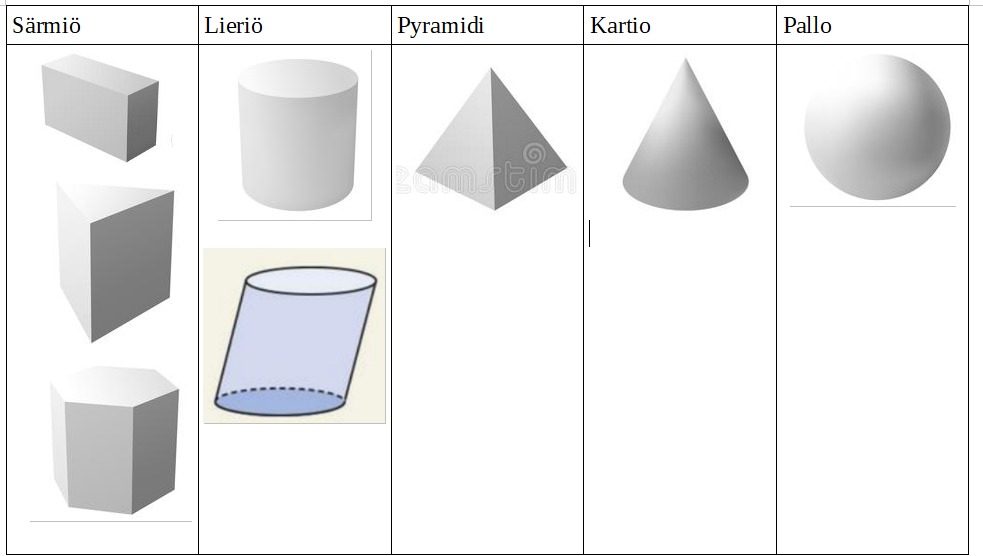
Opetellaan niihin liittyviä mittoja, pinta-aloja ja tilavuuksia.
4.1. Särmiö
Tilavuus:

Siis särmiän tilavuus on pohjan ala · korkeus
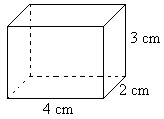
Kuvan särmiössä on
Pohjan ala 4cm·2cm = 8 cm²
Korkeus h = 3 cm
Tilavuus V = 8 cm²·3 cm = 24 cm³
Lävistäjä:

Lävistäjä d lasketaan Pythagoraan lauseella:
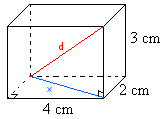
Kuvan särmiössä on
Pohjan lävistäjän neliö: x² = 4²+2² = 20 (cm²)
Särmiön lävistäjän neliö: d² = x² + 3² =20 + 9 = 29 (cm²)
Särmiön lävistäjä: [[$ d=\sqrt{29} $]]=5,3852
Vastaus: 5,4 cm
Sivun 130 tehtävien ratkaisuja: MAB03sivu130.pdf
4.2. Lieriö

Tilavuus = pohjan ala · korkeus
[[$ V=Ah = \pi r^2 h $]]

Pystyseinä on vaippa. Kun sen oikaisee, on se suorakulmio.
Vaipan ala [[$ A_v = 2 \pi r h $]]
Koko lieriön ala on vaipan ala + 2 kertaa pohjan ala.
Esimerkki:
Lieriön pohja on ympyrä, jonka säde on 10 cm, ja korkeus on 15 cm.
a) Tilavuus [[$ V = \pi r^2 h = \pi \cdot (10cm)^2 \cdot 15cm = 5712,39 cm^3 \approx 5700 cm^3 $]]
b) Vaipan ala [[$ A_v = 2 \pi rh = 2 \pi \cdot 10cm \cdot 15cm = 942,48cm^2 \approx 940cm^2 $]]
c) Koko lieriön pinta-ala [[$ A = A_{vaippa} + 2 \cdot A_{pohja} $]]
[[$ A_{vaippa} = 942,48cm^2 \\ A_{pohja} = \pi \cdot (10cm)^2 = 314,16cm^2 \\A = 942,48cm^2 + 2 \cdot 314,16cm^2 = 1570,80cm^2 \approx 1600cm^2 $]]
Esimerkki:
Pöntössä 100 litraa vettä nousi 50 cm korkeudelle. Kuinka suuri oli pohjan halkaisija?
Yksi litrahan on 1 dm³ , joten lasketaan desimetreillä.
V = 100 dm³ , h = 5 dm
V = Ah, joten A = V/h = 100 dm³/5dm = 20 dm²
Koska [[$ A = \pi r^2 $]], on
[[$ r^2= \frac{A}{\pi} = \frac{20dm^2}{\pi} = 6,366dm^2 $]]
[[$ r = \sqrt{ 6,366} dm = 2,523dm $]]
Halkaisija on [[$ 2\cdot r = 5,046dm \approx{50 cm} $]]
Sivun 138 tehtävien ratkaisuja: MAB03sivu138.pdf
4.3. Pyramidi

Pyramidin tilavuus: Volyme of ... YouTube
Siis pyramidin tilavuus on kolmasosa särmiön tilavuudesta:
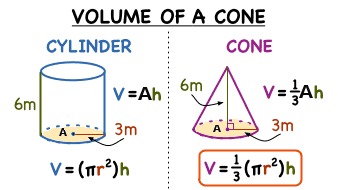
[[$ V=\frac{1}{3} \cdot A_{pohja} \cdot h $]]
Esimerkki:

Tämän pyramidin tilavuuteen tarvitaan
pohjan ala A = 30mm · 65mm = 1950mm²
korkeus, joka onkin hauskempi juttu
Pohjan lävistäjä Pythagoraan lauseella:

[[$ d^2=30^2+65^2 = 5125 \\ d=\sqrt{5125}=71,589 $]]
Sen puolikas on 71,589/2 = 35,795
Korkeus taas Pythagoraan lauseella:

[[$ h^2 = 50^2 - 35,795^2 = 2428,41 \\ h = \sqrt{2484,41} = 49,28 (mm) $]]
Nyt tilavuus on [[$ \frac{1}{3} \cdot 1950 mm^2 \cdot 49,28mm = 32031,29mm^3 \approx 32000mm^3 = 32cm^3 $]]
Entäs sivusärmän ja pohjan välinen kulma?
Se on äskeisessä kolmiossa:

Nyt kulman saakin kosinilla:
[[$ cos(\alpha) = \frac{35,795}{50} = 0,7159 \\\alpha = cos^{-1} (0,7159) = 44,283° \approx 44° $]]
4.4. Kartio
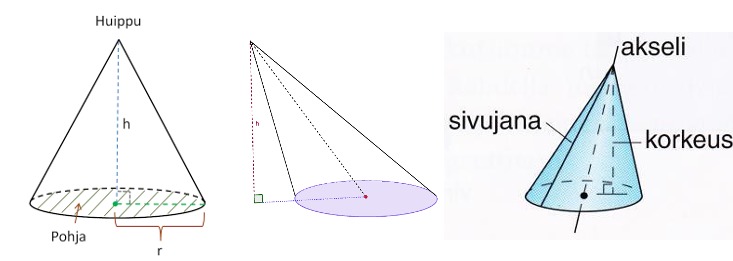
Kartioon liittyviä pinta-aloja:
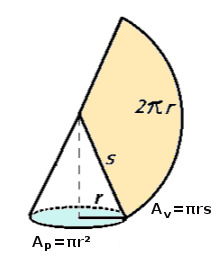
Vanha tuttu: Pohjan ala: [[$ A_{p} = \pi r^2 $]]
Vaippa on ympyrän sektori
- säde: sivujana s
- kaari: pohjan ympärys [[$ 2 \pi r $]]
- ala: [[$ A_v =\pi r s $]]
Koko kartion pinta-ala on pohjan ala + vaipan ala
Kartion tilavuus on kolmasosa lieriön tilavuudesta:
Esimerkki:
Kuvan kartion tilavuus [[$ V= \frac{1}{3}\cdot \pi \cdot (3m)^2 \cdot 6m = 56,548 m^3 \approx 57 m^3 $]]
Vaipan alaa varten pitää laskea sivujana [[$ s^2=3^2+6^2 = 45 \\ s = \sqrt{45} = 6,708 (m) $]]
Nyt [[$ A_v = \pi \cdot 3m \cdot 6,708m = 63,221m^2 \approx 63m^2 $]]
Kurssissa käsitellään seuraavia avaruuskappaleita:

Opetellaan niihin liittyviä mittoja, pinta-aloja ja tilavuuksia.
4.1. Särmiö
Tilavuus:

Siis särmiän tilavuus on pohjan ala · korkeus

Kuvan särmiössä on
Pohjan ala 4cm·2cm = 8 cm²
Korkeus h = 3 cm
Tilavuus V = 8 cm²·3 cm = 24 cm³
Lävistäjä:

Lävistäjä d lasketaan Pythagoraan lauseella:
- Pohjan lävistäjä x: [[$ x^2=a^2+b^2 $]]
- Särmiön lävistäjä d: [[$ d^2=x^2+c^2 $]]=[[$ x^2=a^2+b^2+c^2 $]]
- Siispä

Kuvan särmiössä on
Pohjan lävistäjän neliö: x² = 4²+2² = 20 (cm²)
Särmiön lävistäjän neliö: d² = x² + 3² =20 + 9 = 29 (cm²)
Särmiön lävistäjä: [[$ d=\sqrt{29} $]]=5,3852
Vastaus: 5,4 cm
Sivun 130 tehtävien ratkaisuja: MAB03sivu130.pdf
4.2. Lieriö

Tilavuus = pohjan ala · korkeus
[[$ V=Ah = \pi r^2 h $]]

Pystyseinä on vaippa. Kun sen oikaisee, on se suorakulmio.
Vaipan ala [[$ A_v = 2 \pi r h $]]
Koko lieriön ala on vaipan ala + 2 kertaa pohjan ala.
Esimerkki:
Lieriön pohja on ympyrä, jonka säde on 10 cm, ja korkeus on 15 cm.
a) Tilavuus [[$ V = \pi r^2 h = \pi \cdot (10cm)^2 \cdot 15cm = 5712,39 cm^3 \approx 5700 cm^3 $]]
b) Vaipan ala [[$ A_v = 2 \pi rh = 2 \pi \cdot 10cm \cdot 15cm = 942,48cm^2 \approx 940cm^2 $]]
c) Koko lieriön pinta-ala [[$ A = A_{vaippa} + 2 \cdot A_{pohja} $]]
[[$ A_{vaippa} = 942,48cm^2 \\ A_{pohja} = \pi \cdot (10cm)^2 = 314,16cm^2 \\A = 942,48cm^2 + 2 \cdot 314,16cm^2 = 1570,80cm^2 \approx 1600cm^2 $]]
Esimerkki:
Pöntössä 100 litraa vettä nousi 50 cm korkeudelle. Kuinka suuri oli pohjan halkaisija?
Yksi litrahan on 1 dm³ , joten lasketaan desimetreillä.
V = 100 dm³ , h = 5 dm
V = Ah, joten A = V/h = 100 dm³/5dm = 20 dm²
Koska [[$ A = \pi r^2 $]], on
[[$ r^2= \frac{A}{\pi} = \frac{20dm^2}{\pi} = 6,366dm^2 $]]
[[$ r = \sqrt{ 6,366} dm = 2,523dm $]]
Halkaisija on [[$ 2\cdot r = 5,046dm \approx{50 cm} $]]
Sivun 138 tehtävien ratkaisuja: MAB03sivu138.pdf
4.3. Pyramidi

Pyramidin tilavuus: Volyme of ... YouTube
Siis pyramidin tilavuus on kolmasosa särmiön tilavuudesta:
[[$ V=\frac{1}{3} \cdot A_{pohja} \cdot h $]]
Esimerkki:

Tämän pyramidin tilavuuteen tarvitaan
pohjan ala A = 30mm · 65mm = 1950mm²
korkeus, joka onkin hauskempi juttu
Pohjan lävistäjä Pythagoraan lauseella:

[[$ d^2=30^2+65^2 = 5125 \\ d=\sqrt{5125}=71,589 $]]
Sen puolikas on 71,589/2 = 35,795
Korkeus taas Pythagoraan lauseella:

[[$ h^2 = 50^2 - 35,795^2 = 2428,41 \\ h = \sqrt{2484,41} = 49,28 (mm) $]]
Nyt tilavuus on [[$ \frac{1}{3} \cdot 1950 mm^2 \cdot 49,28mm = 32031,29mm^3 \approx 32000mm^3 = 32cm^3 $]]
Entäs sivusärmän ja pohjan välinen kulma?
Se on äskeisessä kolmiossa:

Nyt kulman saakin kosinilla:
[[$ cos(\alpha) = \frac{35,795}{50} = 0,7159 \\\alpha = cos^{-1} (0,7159) = 44,283° \approx 44° $]]
4.4. Kartio

Kartioon liittyviä pinta-aloja:

Vanha tuttu: Pohjan ala: [[$ A_{p} = \pi r^2 $]]
Vaippa on ympyrän sektori
- säde: sivujana s
- kaari: pohjan ympärys [[$ 2 \pi r $]]
- ala: [[$ A_v =\pi r s $]]
Koko kartion pinta-ala on pohjan ala + vaipan ala
Kartion tilavuus on kolmasosa lieriön tilavuudesta:

Esimerkki:
Kuvan kartion tilavuus [[$ V= \frac{1}{3}\cdot \pi \cdot (3m)^2 \cdot 6m = 56,548 m^3 \approx 57 m^3 $]]
Vaipan alaa varten pitää laskea sivujana [[$ s^2=3^2+6^2 = 45 \\ s = \sqrt{45} = 6,708 (m) $]]
Nyt [[$ A_v = \pi \cdot 3m \cdot 6,708m = 63,221m^2 \approx 63m^2 $]]