The zero exponent
Next, let’s look at the division [[$ \dfrac{4^3}{4^3} $]] in two different ways. Let's simplify by the quotient of equal powers and by reducing.
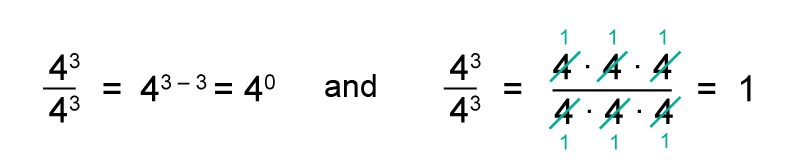
Since both actions are allowed, the results must be equal. In other words, [[$ 4^0 = 1 $]].
b) [[$ -45^0 = -1 $]]
c) [[$ 0^0 $]] cannot be calculated
d) [[$ \dfrac{a^3 \cdot a^9}{a^{12}} = \dfrac{a^{3+9}}{a^{12}} = \dfrac{a^{12}}{a^{12}} = a^{12-12} =a^0 = 1 $]]
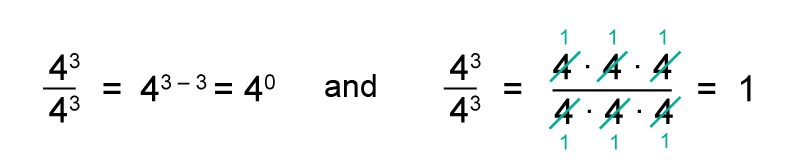
Since both actions are allowed, the results must be equal. In other words, [[$ 4^0 = 1 $]].
Zero as an exponent
If there is a zero as an exponent, the value of the power is always 1. The base number can never be zero.
[[$ a^0 = 1 \text{, kun } a \neq 0. $]]
Example 3
Simplify the powers.
a) [[$ 99^0 = 1 $]]b) [[$ -45^0 = -1 $]]
c) [[$ 0^0 $]] cannot be calculated
d) [[$ \dfrac{a^3 \cdot a^9}{a^{12}} = \dfrac{a^{3+9}}{a^{12}} = \dfrac{a^{12}}{a^{12}} = a^{12-12} =a^0 = 1 $]]