8. Calculating powers with a calculator
Exercises
Calculating powers with a calculator
Even if you have a calculator at your disposal, you still need to master the rules for calculating powers. If the power is too high for the calculator to handle, you must be able to convert it into a form the calculator can use. In addition, you must know how to interpret the printouts given by the calculator correctly. Because of the wide variety of calculators, the operating instructions should also be retained for future reference.
Example 1
Calculate the approximate number of [[$ 2^{60} $]] with a calculator. How many digits are there in the number [[$ 2^{60} $]]?
By entering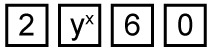 
in the calculator, the number 
is displayed. This result can look somewhat different depending on your calculator.
The result contains too many numbers to fit completely on the screen, so the calculator displays its approximate value as a scientific expression. The result is interpreted as follows:[[$ 2^{60} \approx \text{1.152921} \cdot 10^{18} $]]. The scientific expression can be converted into an ordinary number as follows:
[[$ 2^{60} \approx \text{1,152921} \cdot 10^{18} = \text{1.152921} \cdot \underbrace{1000000000000000000}_{1 \text{ and } 18 \text{ zeros}} = 1152921000000000000 $]]
The approximation is [[$ \text{1.152921} \cdot 10^{18} $]], and the number has a total of 19 digits.
Example 2
Calculate the approximate value of [[$ 5^{250} $]] at the accuracy of two decimal places. How many digits are there in number [[$ 5^{250} $]]?
Since most calculators cannot handle such big powers, the power must be divided into parts.
The approximate value is [[$ \text{5.5} \cdot 10^{174} $]] and the number has 175 digits.
N.B! Remember that the multiplier of a scientific expression is always between 1-10.
Example 3
Calculate the following expression with a calculator: [[$ \text{2.3} \cdot 10^9 + \text{1.6} \cdot 10^{10} $]].
Scientific expressions can be entered into the calculator by using the EXP button.
By entering 
in the calculator, the result
will appear on the screen.
Therefore, the answer is [[$ \text{1.83} \cdot 10^{10} $]].