17.11 S.48-49
Matemaattinen malli= Suureiden välisiä riippuvuuksia, ja sitä ilmaistaan suureyhtälöiden avulla.
Lineaarinen malli= Kun suureita kuvataan suoralla.
Fysikaalinen kulmakerroin= m=kV
Aineetiheyden matemaattinen malli=
Fysikaalisen kulmakertoimen määritys:
Kuvaaja esittää erään aineen massan tilavuuden funktiona. Määritä kuvaajan avulla aineen
a) massa, kun sen tilavuus on 25 cm3
- n. 310 g
b) tilavuus, kun sen massa on 400 g
- n. 32 cm3
c) tiheys

5-2
Taulukossa esitetään alumiinikappaleiden ja vesimäärien tilavuudet ja massat 20°C:een lämpötilassa.
a) Esitä mittaustulokset V,m-koordinaatistossa.
Alumiini:
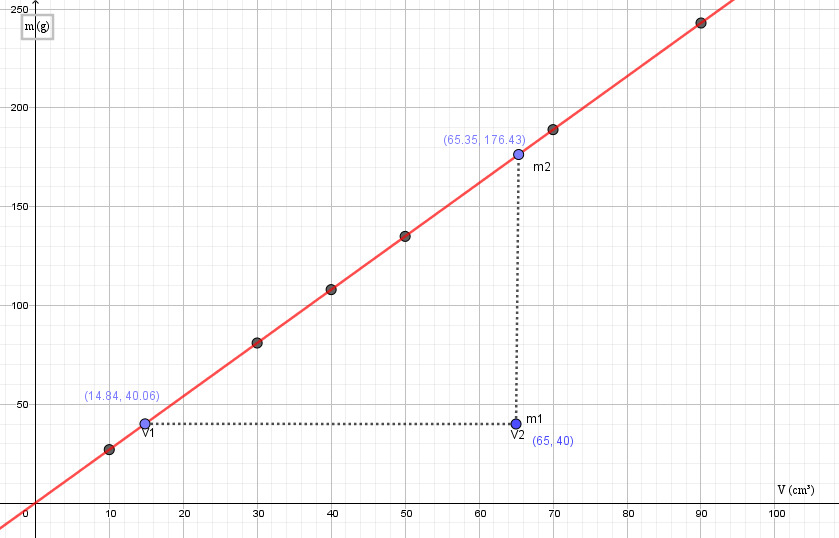
Vesi:
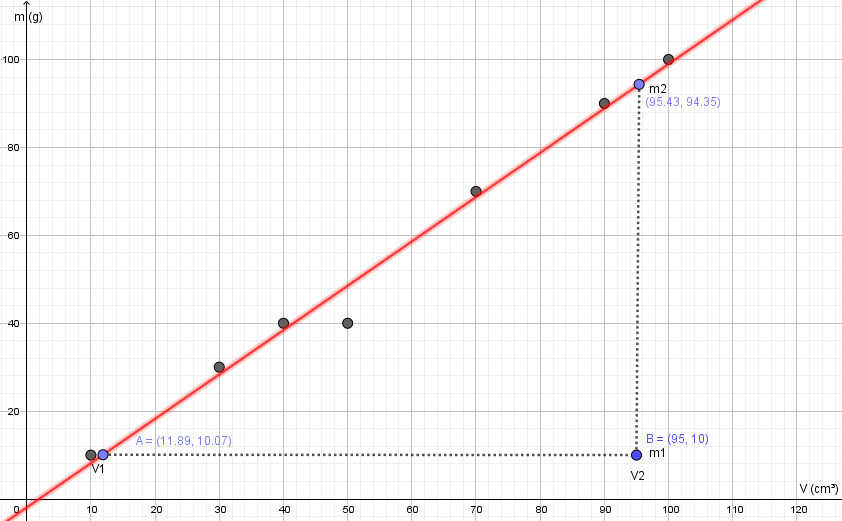
b) Määritä kuvaajien alumiinin ja veden tiheydet.
Alumiini:
Vesi:

c) Ilmoita tiheydet käyttäen yksikköä kg/m3
2,7g/cm3= 2700 kg/m3
1,0g/cm3= 1000kg/m3
5-3
5-6
Tehtävänä oli pmäärittää pienen kiven tiheys. Kiven massaksi mitattiin vaa'alla 150 g ja tilavuudeksi ylivuotoastian avulla 48 cm3.
a) Laske kiven tiheys

b) Ilmoita tiheys käyttäen yksikköä kg/m3.
3,125 g/cm3= 3125 kg/m3
5-7
5-8
Kuinka suuren tilavuuden vie 5,5 kg nestemäistä elohopeaa? Elohopean tiheys on 13 540 kg/m3.

)
5-10
Laboratoriotyössä asetonia kaadetaan vaa'alle asetettuun mittalasiin. Taulukossa on ilmoitettu asetonin määrä mittalasissa ja vaa'an lukema (mitattu massa).
a) Piirrä kuvaaja, joka esittää massan riippuvuutta asetonin tilavuudesta.
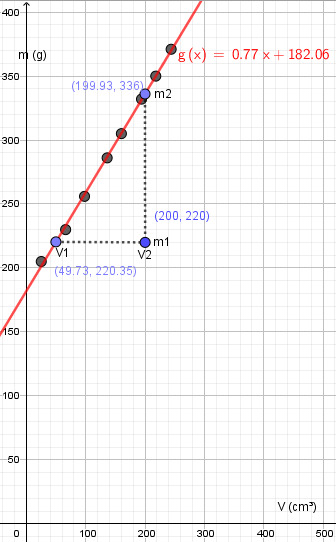
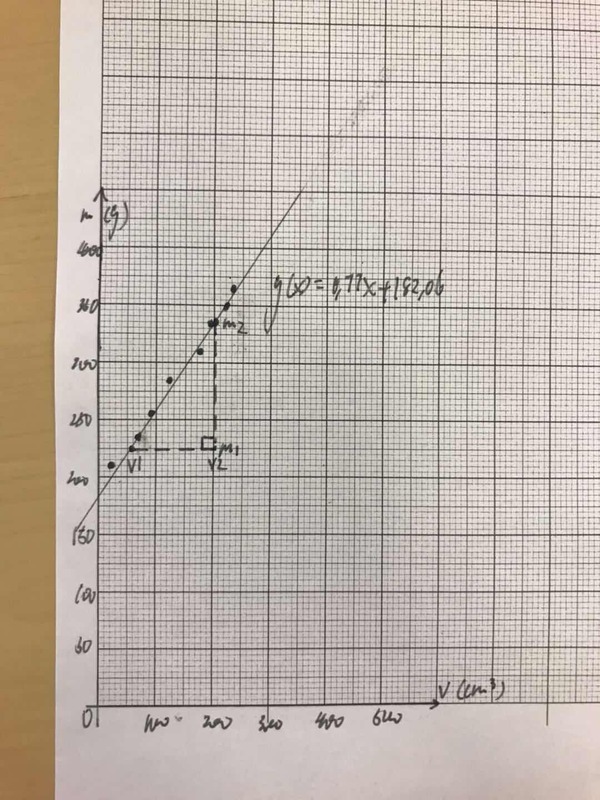
b) Määritä kuvaajan avulla asetonin tiheys.
- 0,77g/cm3
c) Kuinka suuri on tyhjän mittalasin massa?
- Kuvaajasta katsoen vaakasta saattiin lukemia vastaan yli noin 180 g tasosta.
Joten voidaan päätellä, että mittalsin massa on alle 200g, ja se saadaan vähentämällä 25 g ensimmäisestä lukemasta
eli:
205cm3-25g=180g
5-12
Tunnilla tutkittiin, miten kumilenkkiä venyttävä voima F ja kumilenkin venymä x riippuvat toisistaan. Mittaustulokset ovat taulukossa. Määritä kumilenkin ns. jousivakio. Saat sen x,F-koordinaatistosta kuvaajan fysikaalisena kulmakertoimena.
-
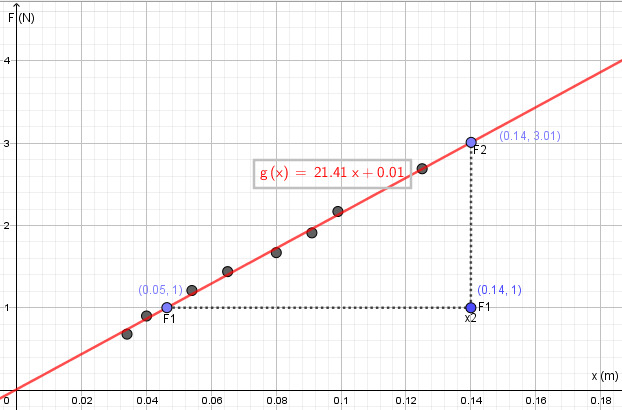
v: n. 21 N/m
Lineaarinen malli= Kun suureita kuvataan suoralla.
Fysikaalinen kulmakerroin= m=kV
Aineetiheyden matemaattinen malli=
Fysikaalisen kulmakertoimen määritys:
- Valitse suoralta kaksi pistettä. Pisteiden tulisi olla kaukana toisistaan sillä mitä kauempana pisteet ovat, sitä tarkemmin kulmakertoimen arvo saadaan määritettyä. Jos suora kulkee origon kautta, toinen pisteistä voi olla origo.
- Koska mitatut pisteet eivät välttämättä ole piirretyllä suoralla, mitattuja (taulukoituja) arvoja ei saa käyttää fysikaalisen kulmakertoimen määrittämisessä.
- V, m-koordiaatistossa fysikaalinen kulmakerroin lasketaan määrittämällä suhde
- Suureen muutos lasketaan aina vähentämällä suureen loppuarvosta suureen alkuarvo.
Kuvaaja esittää erään aineen massan tilavuuden funktiona. Määritä kuvaajan avulla aineen
a) massa, kun sen tilavuus on 25 cm3
- n. 310 g
b) tilavuus, kun sen massa on 400 g
- n. 32 cm3
c) tiheys
5-2
Taulukossa esitetään alumiinikappaleiden ja vesimäärien tilavuudet ja massat 20°C:een lämpötilassa.
a) Esitä mittaustulokset V,m-koordinaatistossa.
Alumiini:

Vesi:

b) Määritä kuvaajien alumiinin ja veden tiheydet.
Alumiini:
Vesi:
c) Ilmoita tiheydet käyttäen yksikköä kg/m3
2,7g/cm3= 2700 kg/m3
1,0g/cm3= 1000kg/m3
5-3
5-6
Tehtävänä oli pmäärittää pienen kiven tiheys. Kiven massaksi mitattiin vaa'alla 150 g ja tilavuudeksi ylivuotoastian avulla 48 cm3.
a) Laske kiven tiheys
b) Ilmoita tiheys käyttäen yksikköä kg/m3.
3,125 g/cm3= 3125 kg/m3
5-7
5-8
Kuinka suuren tilavuuden vie 5,5 kg nestemäistä elohopeaa? Elohopean tiheys on 13 540 kg/m3.
5-10
Laboratoriotyössä asetonia kaadetaan vaa'alle asetettuun mittalasiin. Taulukossa on ilmoitettu asetonin määrä mittalasissa ja vaa'an lukema (mitattu massa).
| m (g) | V (cm3) |
| 25 | 205 |
| 66 | 230 |
| 98 | 256 |
| 136 | 286 |
| 160 | 305 |
| 194 | 332 |
| 218 | 350 |
| 244 | 371 |


b) Määritä kuvaajan avulla asetonin tiheys.
- 0,77g/cm3
c) Kuinka suuri on tyhjän mittalasin massa?
- Kuvaajasta katsoen vaakasta saattiin lukemia vastaan yli noin 180 g tasosta.
Joten voidaan päätellä, että mittalsin massa on alle 200g, ja se saadaan vähentämällä 25 g ensimmäisestä lukemasta
eli:
205cm3-25g=180g
5-12
Tunnilla tutkittiin, miten kumilenkkiä venyttävä voima F ja kumilenkin venymä x riippuvat toisistaan. Mittaustulokset ovat taulukossa. Määritä kumilenkin ns. jousivakio. Saat sen x,F-koordinaatistosta kuvaajan fysikaalisena kulmakertoimena.
| x(m) | 0,034 | 0,040 | 0,054 | 0,065 |
| F(N) | 0,68 | 0,90 | 1,21 | 1,44 |
| x(m) | 0,080 | 0,091 | 0,099 | 0,125 |
| F(N) | 1,67 | 1,91 | 2,17 | 2,69 |

v: n. 21 N/m