Numeeriset menetelmät
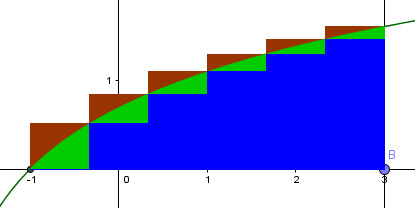
Integrointi, yläsumma ja alasumma
Regressio
Mene taulukkolaskentanäkymään ja luo kaksisarakkeinen pistejoukko. Muista, että desimaalipilkun sijaan käytetään desimaalipistettä. Maalaa pisteistö ja oikealla hiirennapilla pisteistön päällä saat valikon, josta löytyy Luo -> Pistelista.
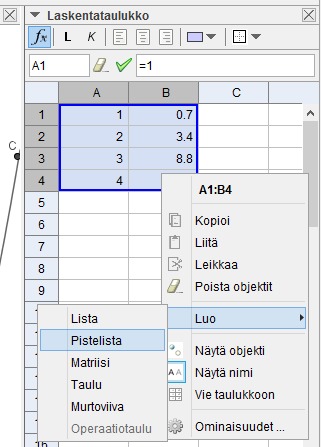
Kirjoita kaavariville sopiva regressio funktio, esim polynominen: SovitaPolynomi(lista1,2). Ensimmäinen parametri on listasi nimi, eli tässä lista1. Toinen parametri on polynomin asteluku, tässä 2.
Pistejoukon poikkeamien neliöiden summan saat kaavalla NeliöSummaVirhe(L,f), missä L on pistejoukko ja f on funktio, johon pistejoukkoa sovitetaan.
Taylorin sarja
Käytä komentorivisyötettä TaylorSarja( ln(x+1), 1, 3 ). Ensimmäinen parametri ln(x+1) on funktio, josta sarja muodostetaan, seuraava 1 on kohta jossa approksimaatio tehdään ja viimeinen 3 on sarjan asteluku, eli tässä tapauksessa kolmannen asteen Taylorin polynomi.
- Integraali lasketaan komennolla Integraali(f,a,b), missä f on integroitava funktio ja a ja b ovat välin päätepisteet
- Alasumma(f,a,b,n) Alasumman kaavassa on lisäksi n, joka kertoo suorakulmioiden lukumäärän.
- Yläsumma(f,a,b,n). Kuten alasumma.

Regressio
Mene taulukkolaskentanäkymään ja luo kaksisarakkeinen pistejoukko. Muista, että desimaalipilkun sijaan käytetään desimaalipistettä. Maalaa pisteistö ja oikealla hiirennapilla pisteistön päällä saat valikon, josta löytyy Luo -> Pistelista.

Kirjoita kaavariville sopiva regressio funktio, esim polynominen: SovitaPolynomi(lista1,2). Ensimmäinen parametri on listasi nimi, eli tässä lista1. Toinen parametri on polynomin asteluku, tässä 2.
Pistejoukon poikkeamien neliöiden summan saat kaavalla NeliöSummaVirhe(L,f), missä L on pistejoukko ja f on funktio, johon pistejoukkoa sovitetaan.
Taylorin sarja
Käytä komentorivisyötettä TaylorSarja( ln(x+1), 1, 3 ). Ensimmäinen parametri ln(x+1) on funktio, josta sarja muodostetaan, seuraava 1 on kohta jossa approksimaatio tehdään ja viimeinen 3 on sarjan asteluku, eli tässä tapauksessa kolmannen asteen Taylorin polynomi.