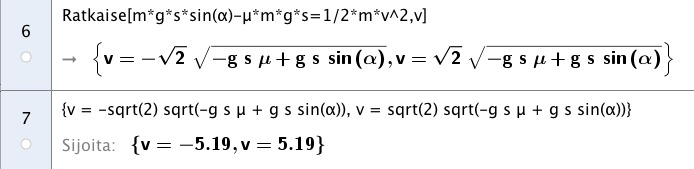K2014 T5

Ratkaisu a-kohtaan

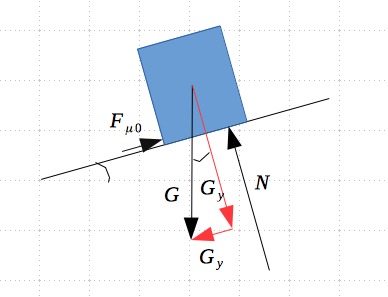
Piirretään lumipaakku ja siihen kohdistuvat voimat.

Paakku on levossa, joten N2 mukaan

$\sum_{ }^{ }\vec{F}=m\vec{a}=\vec{0}$

Tehdään voimatarkastelu x- ja y-suunnassa

x: $\sum_{ }^{ }F_x=0$ eli $G_x-F_{\mu0}=0$ eli $G\sin\alpha-\mu_0N=0$

y: $\sum_{ }^{ }F_y=0$ eli $N-G\ \cos\alpha=0$

Ratkaistaan lepokitkakerroin laskinohjelmiston avulla.

Vastaus: Lepokitkakerroin on noin 0,47

Ratkaisu b-kohtaan

Olkoon potentiaalienergian nollataso korkeudella, jolla paakku on liu'uttuaan s=4,0 m.

Lähtökorkeus h voidaan kirjoittaa nyt

$h=s\cdot\sin\left(\alpha\right)$

Kitka tekee työtä joten mekaniikan energiaperiaatteen mukaan

$mgh-W=\frac{1}{2}mv^2$
$mgh-\mu mg\cdot s=\frac{1}{2}mv^2$
$mg\cdot s\cdot\sin\alpha-\mu mg\cdot s=\frac{1}{2}mv^2$

Ratkaistaan loppunopeus v laskinohjelmiston avulla.

Vastaus: noin 5,2 m/s