Yhtälöitä ja yhtälöryhmiä voi ratkaista symbolisen laskennan ohjelmistojen tai symbolisen laskimen avulla (CAS-laskin). Ohjelmistoja käyttämällä voi ratkaista tehtävän tai tarkistaa vastauksen. Ohjelmistojen oikeanlainen käyttö säästää aikaa monimutkaisessa tehtävässä. Laskennallisessa tehtävässä ratkaistaan lauseke tuntemattomalle suureelle eli pelkkä numeerinen ratkaisu ei riitä täysiin pisteisiin.

Ohjelmiston käyttö osana vastausta

• Tilannetta kuvaavat yhtälöt esitetään yleisessä muodossa ja perusteltuna.
• Mainitaan, että ohjelmistoa hyödynnetään ratkaisussa ja liitetään mielellään kuvankaappaus ohjelmistosta.
• Ilmoitetaan ohjelmiston antama ratkaistu lauseke.

Alla ovat esimerkit yhtälön ratkaisusta sekä yhtälöparin ratkaisusta GeoGebran CAS-laskin ohjelmistolla.

Yhtälön ratkaisu GeoGebralla

Tarkastellaan tilannetta, jossa kappale on tasaisesti kiihtyvässä liikkeessä. Kappale lähtee liikkeelle levosta. Kappalen kiihtyvyys on [[$2{,}5 \ \mathrm{m/s^2}$]] ja kulkema matka [[$28 \ \mathrm{m}$]]. Taulukkokirjasta saadaan kaava paikalle tasaisesti kiihtyvässä liikkeessä.

Paikka tasaisesti kiihtyvässä liikkeessä
[[$ x=\dfrac{1}{2}at^2 $]]

Ratkaistaan yhtälöstä aika [[$t$]] GeoGebran CAS -ympäristössä. GeoGebra ratkaisee yhtälön muuttujan [[$t$]] suhteen ja antaa vastauksen. Vastauksen muoto noudattaa matemaattista esitystapaa, jossa nimittäjässä ei esiinny neliöjuuressa olevaa lauseketta. Käsin laskemalla päädytään usein muotoon [[$ t=\sqrt{\dfrac{2x}{a}} $]]​. Vaikka lausekkeet näyttävät erilaisilta, ovat samat. GeoGebra antaa ratkaisuksi ajalle myös negatiivisen lausekkeen. Fysiikassa negatiiivinen ratkaisu on epämielekäs tulos, eikä sitä tarvitse huomioida, jos se on itsestään selvää.

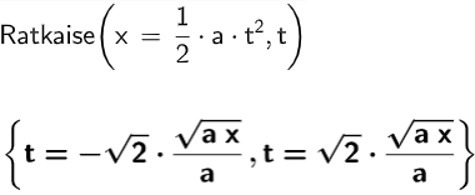
Kun ratkaisu kirjoitetaan GeoGebran CAS-laskimessa huomioi seuraavat asiat.

• Desimaalierotin on piste. Pilkkua käytetään komentojen sisällä osien erotteluun. Luku puoli (1/2) kirjoitetaan GeoGebrassa muotoon 0.5, EI MUODOSSA 0,5.
• Kahden muuttujan tulo kirjoitetaan aina kertomerkkiä käyttäen tai muuttujien väliin kirjoiteaan välilyönti. Ajan ja nopeuden tulo kirjoitetaan muodossa "v*t" tai "v t", EI MUODOSSA "vt". Yhteenkirjoitettuna "vt" tarkoitta GeoGebrassa suuretta, jonka tunnus on [[$vt$]].

GeoGebralla voi ratkaista liikkeeseen kuluvan ajan suuruuden sijoita komennolla. Komennon avulla aukeaa taulukko, johon lähtöarvot sijoitetaan. Lukuarvot sijoitetaan desimaalipistettä käyttäen. Noin merkistä painamalla saadaan desimaalimuotoinen vastaus. Vastauksen tarkkuus määrätään asetuksista. Vastauksen tarkkuuden voi valita desimaalien tai merkitsevien numeroiden mukaan.

Taulukko ei kelpaa suureiden suuruuksien perusteluiksi, vaan lukuarvot on kirjoitettava erikseen vastaukseen.

[[$a=2{,}5 \ \mathrm{m/s^2}$]]
[[$x=28 \ \mathrm{m}$]]

[[$t=4{,}7333 \ \mathrm{s}\approx 4{,}7 \ \mathrm{s}$]]

---

Yhtälöryhmän ratkaisu GeoGebralla

 Ratkaistaan aika ja kiihtyvyys tasaisesti kiihtyvän liikkeen yleisistä yhtälöistä​[[$ s=v_0 t+\dfrac{1}{2}at^2 $]]​ ja [[$ v=v_0+at $]]​​.

Yhtälöryhmä tai yhtälöpari ratkaistaan Ratkaise-komennolla siten, että yhtälöt sekä muuttujat sijoitetaan aaltosulkeiden sisään ja erotetaan toisistaan pilkulla. Lukuarvon laskeminen tehdään samalla tavalla kuin yhden yhtälön tapauksessa edellä tehtiin.