MAA5 Vektorit
Mikä on vektori?
Johdanto
 Vektori on matemaattinen olio, jolla voidaan kuvata siirtymää. Vektorilla on suunta ja pituus.
Vektori on matemaattinen olio, jolla voidaan kuvata siirtymää. Vektorilla on suunta ja pituus.
Graafisesti vektoria kuvaa nuoli. Useissa fysiikan sovelluksissa vektoria voidaan käyttää myös kuvaamaan tietyn suuruista voimaa, joka vaikuttaa tiettyyn suuntaan. Tällöin vektorin pituus on kyseinen voima. Liikkuvan kappaleen nopeutta voidaan kuvata myös vektorilla, tällöin suunta ilmaisee, mihin suuntaan kappale liikkuu ja vektorin pituus kuvaa vauhtia, yksikkönä vaikkapa m/s.
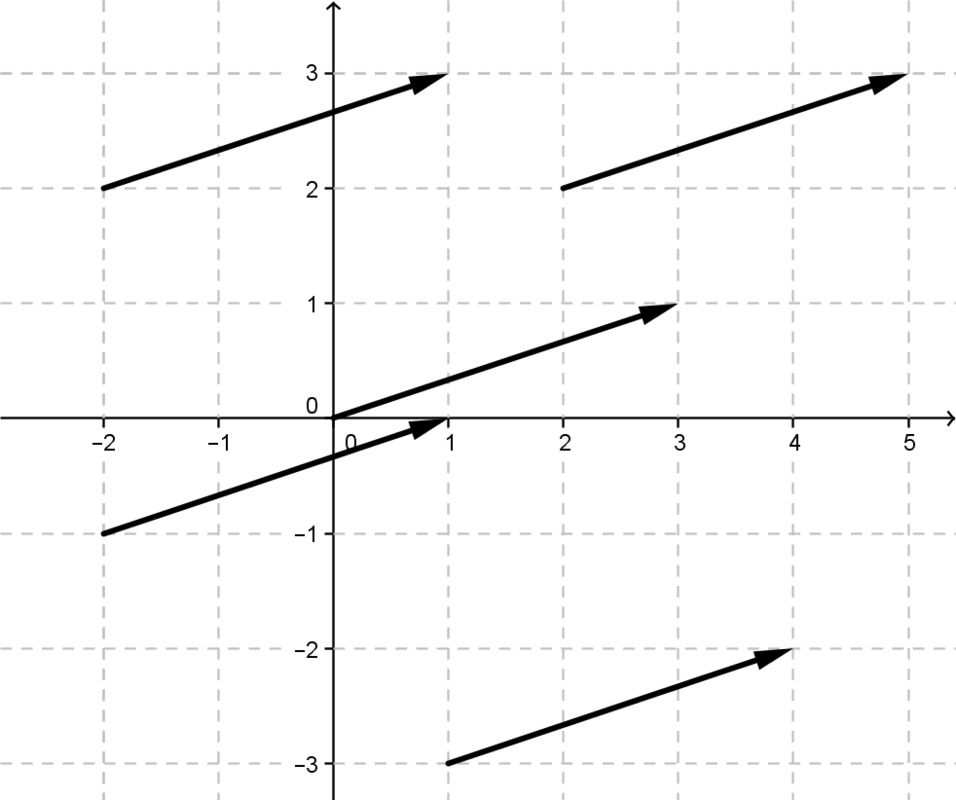
Vektorin kannalta ei ole merkitystä, mistä pisteestä se alkaa, koska vektoriin liittyy vain suunta ja pituus. Kaikki saman suuntaiset ja yhtä pitkät nuolet edustavat samaa vektoria. Kuvassa on esitetty joukko vektoreita, jotka kaikki esittävät siirtymää "kolme oikeaan ja yksi ylös".
Merkinnät
Matematiikassa lukuja esitetään kirjainsymboleilla, ja kun halutaan kertoa, että kyseessä on vektori, eikä pelkkä luku, liitetään kirjaimen yläpuolelle viiva, tai nuoli. Merkintä [[$\vec{a}$]] tai [[$\overline{a}$]] luetaan: "Vektori a".
Vektorin pituutta merkitään itseisarvomerkeillä. Voidaan ajatella, että vektorin itseisarvo vastaa vektorin pituutta. Matematiikassa vektorin normi tarkoittaa samaa kuin vektorin pituus.
- [[$\overline{a}= \text{vektori}$]]
- [[$|\overline{a}|= \text{vektorin }\overline{a}\text{ pituus.}$]]
- [[$\bar a \parallel \bar b \text{: vektorit ovat yhdensuuntaiset}$]]
- [[$\bar a \upuparrows \bar b \text{: vektorit ovat samansuuntaiset}$]]
- [[$\bar a \uparrow \downarrow \bar b \text{: vektorit ovat vastakkaissuuntaiset}$]]
- [[$\bar a \nparallel \bar b \text{: vektorit ovat erisuuntaiset}$]]
Vektorin kertominen luvulla
Vektorien kertominen positiivisella luvulla
 [[$\overline{a}+\overline{a}$]] tarkoittaa siirtymää, joka saadaan tekemällä kaksi kertaa peräkkäin siirtymä [[$\overline{a}$]].
[[$\overline{a}+\overline{a}$]] tarkoittaa siirtymää, joka saadaan tekemällä kaksi kertaa peräkkäin siirtymä [[$\overline{a}$]].
Yleisesti voidaan todeta, että vektoreille pätee [[$k\text{ }\overline{a}=\underbrace{\overline{a}+\overline{a}+\dots+\overline{a}}_\text{k kpl}\text{, }\qquad k\in\mathbb{N}$]].
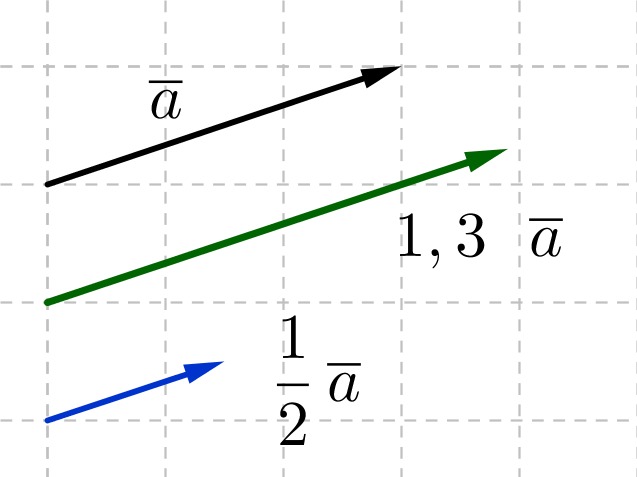 Kun vektori kerrotaan positiivisella luvulla, sen pituus muuttuu ja suunta pysyy samana. Uusi pituus saadaan kertomalla alkuperäisen vektorin pituus kertoimena olleella luvulla.
Kun vektori kerrotaan positiivisella luvulla, sen pituus muuttuu ja suunta pysyy samana. Uusi pituus saadaan kertomalla alkuperäisen vektorin pituus kertoimena olleella luvulla.
Esimerkiksi vektorin [[$\frac{1}{2}\overline{a}$]] pituus on puolet vektorin [[$\overline{a}$]] pituudesta. Kertomalla vektori jollain nollaa suuremmalla luvulla vektoria voidaan kutistaa tai venyttää riippuen siitä onko kerroin suurempi vai pienempi kuin yksi.
- [[$|k\overline{a}|=k|\overline{a}|\text{, }\qquad k>0$]]
- [[$k\overline{a} \upuparrows \overline{a}\text{, }\qquad k>0$]]
Vektorin kertominen negatiivisella luvulla
 Kun vektori kerrotaan negatiivisella luvulla, sen suunta muuttuu vastakkaiseksi. Sanotaan, että vektorin [[$ \bar a $]] vastavektori on [[$-\bar a$]]. Vastavektori on siis miinus yksi kertaa alkuperäinen vektori. Kerrottaessa vektoria negatiivisella luvulla vektorin suunta muuttuu siis vastakkaiseksi ja pituus vastaa vektorin pituutta kerrottuna kertoimen itseisarvolla.
Kun vektori kerrotaan negatiivisella luvulla, sen suunta muuttuu vastakkaiseksi. Sanotaan, että vektorin [[$ \bar a $]] vastavektori on [[$-\bar a$]]. Vastavektori on siis miinus yksi kertaa alkuperäinen vektori. Kerrottaessa vektoria negatiivisella luvulla vektorin suunta muuttuu siis vastakkaiseksi ja pituus vastaa vektorin pituutta kerrottuna kertoimen itseisarvolla.
Vektoreiden yhteen- ja vähennyslasku
Vektoreiden yhteen- ja vähennyslasku
Vektoreiden yhteenlasku tarkoittaa, että siirtymät asetetaan peräkkäin. Esimerkiksi summa [[$\bar a + \bar b$]] tarkoittaa siirtymää, joka syntyy kun ensin siirrytään vektorin [[$\bar a$]] siirtymä ja sen jälkeen vektorin [[$\bar b$]] siirtymä.
Voidaan osoittaa, että
[[$\bar a +\bar b = \bar b + \bar a$]]
Negatiivinen siirtymä tarkoittaa, että vektoria kuljetaan lopusta alkuun, siis nuolen osoittamaa suuntaa vastaan. Vektorin vähentäminen toisesta vektorista on sama asia kuin vastavektorin lisääminen:
[[$\bar a -\bar b = \bar a + (-\bar b)$]]

[[$\bar a + \bar b $]], [[$\bar a - \bar b $]], [[$\bar b + \bar a $]], [[$\bar b - \bar a $]], [[$-\bar b - \bar a $]], [[$-\bar b + \bar a $]], [[$-\bar a + \bar b $]], [[$-\bar a - \bar b $]]