Esimerkit
S.93 10-12
Lasketaan ensin ainemäärä alussa
Oletetaan ilma ideaalikaasuksi, eli
Ainemäärä täytön jälkeen
Ainemäärän muutos
Isobaarinen
Muutos on isobaarinen ja noudattaa Charksin lakia
Isokoorinen
Muutos noudattaa Gay-lusiaan lakia.
Mittari näyttää, kuinka paljon yli normaali -ilmanpaineen paine on eli
Isoterminen
Paine-ero säiliön sisä-ja ulkopuolella tasoittuu, joten säiliön sisäle saadaan normaali-ilmanpaine. Kun lämpötila on vskio, muutos noudattaa Baylen lakia.
Kaasun yleinen tilanyhtälö
Esim. 18l:n säiliössä on happikaasua ( ), jonka lämpötila on 20°C. Säiliön sisällä oleva paine on 9,6 bar. Kuinka paljon säiliössä on kaasua?
), jonka lämpötila on 20°C. Säiliön sisällä oleva paine on 9,6 bar. Kuinka paljon säiliössä on kaasua?




 , josta on ainemäärä on
, josta on ainemäärä on
 Ainemäärällä om
Ainemäärällä om  eli
eli 
Oletetaan, että happikaasu on ideaalikaasu, jolloin on voimassa yhtälö
Mikä on ideaalikaasu? Mikä on ideaali-ja reaalikaasun ero?
- Ideaalikaasu on yksinkertaisin kaasujen mikroskooppinen malli, jossa molekyylt oletetaan pistemäisiksi ja niillä ei ole oleteta olevan törmäyksen lisäksi muita uorovaikutuksia.
Reaalikaasu Ideaalikaasu Monet kaasut ovat seoksia. Puhtaat reaalikaasut koostuvat samoista atomeista tai molekyyleistä. Ideaalikaasussa on vain yhdenlaisia rakenneosia. Molekyylien suurusluoka on 10-10m. Hiukkasiin kohdistuu myös paino. Rakennosat ovat pistemäisiä. Rakenneosasilla on lämpökliikettä; myös virtaukset ovat mahdollisia. Rakenneosasten lämpöliike on satunnaista. Rakenneosasten välillä on sähkömagneettinen vuorovaikutus. Rakenneosaset vuorovaikuttavat vain tötmäysten kautta. Törmäykset voivat olla kimmoisia tai kimmottomia. Rakenneosasten välillä on vain kimmoisia törmäyksiä. Rakenneosasten liike on törmäysten välillä lähes suoraviivaista. Rakennosaset liikuvat törmäysten välillä vkionopeudella ja suoraviivaisesti.
Energian sitoutuminen ja vapautuminen
Esim.
a) Kuinka paljo tarvitaan energiaa, kun 1,45kg kuparia lämmitetään lämpötila 20°C lämpötilaan 65°C?


%7D%3D387%5C%20%5Cfrac%7Bj%7D%7B%5Cleft(kg%5Ccdot%20K%5Cright)%7D)

%7D%5Ccdot1%7B%2C%7D45kg%5Ccdot45K%3D25%7B%2C%7D25175kg%5Capprox25kg)
b) Kuinka paljon nergiaa vapautuu, kun sama määrä vettä jäähtyy lämpötikasta 100°C lämpötilaan 20°C?


%7D)


%7D%5Ccdot1%7B%2C%7D4kg%7D%3D4%7B%2C%7D1563246K)

a) Kuinka paljo tarvitaan energiaa, kun 1,45kg kuparia lämmitetään lämpötila 20°C lämpötilaan 65°C?
Sitoutuva lämpömäärä on
b) Kuinka paljon nergiaa vapautuu, kun sama määrä vettä jäähtyy lämpötikasta 100°C lämpötilaan 20°C?
Veden luovuttaman lämpö on
ja toisaalta
Veden uusi lämpötila on
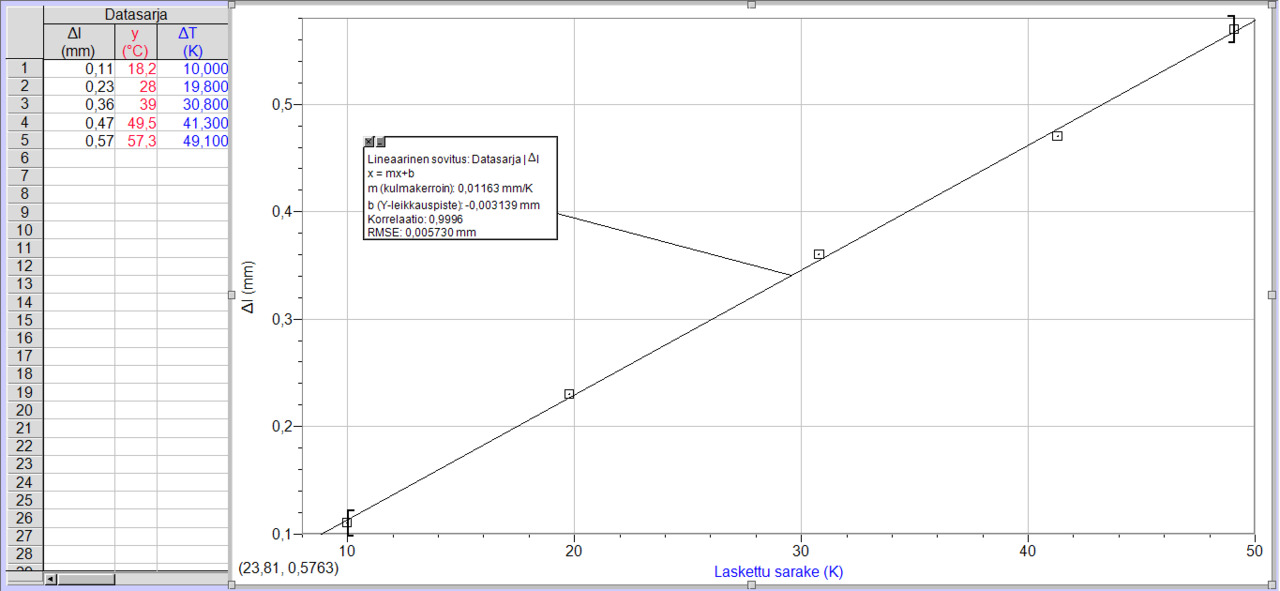
Logger pro
Lämpölaajeneminen
Esim. 1



a)







%3D-0%7B%2C%7D06129864mm)
%3D87%7B%2C%7D25820mm%5Capprox87%7B%2C%7D26mm)
a)
Pituuden muutos lämpötilan kasvaessa
Uusi pituus on siis
b)
Uusi pituus on