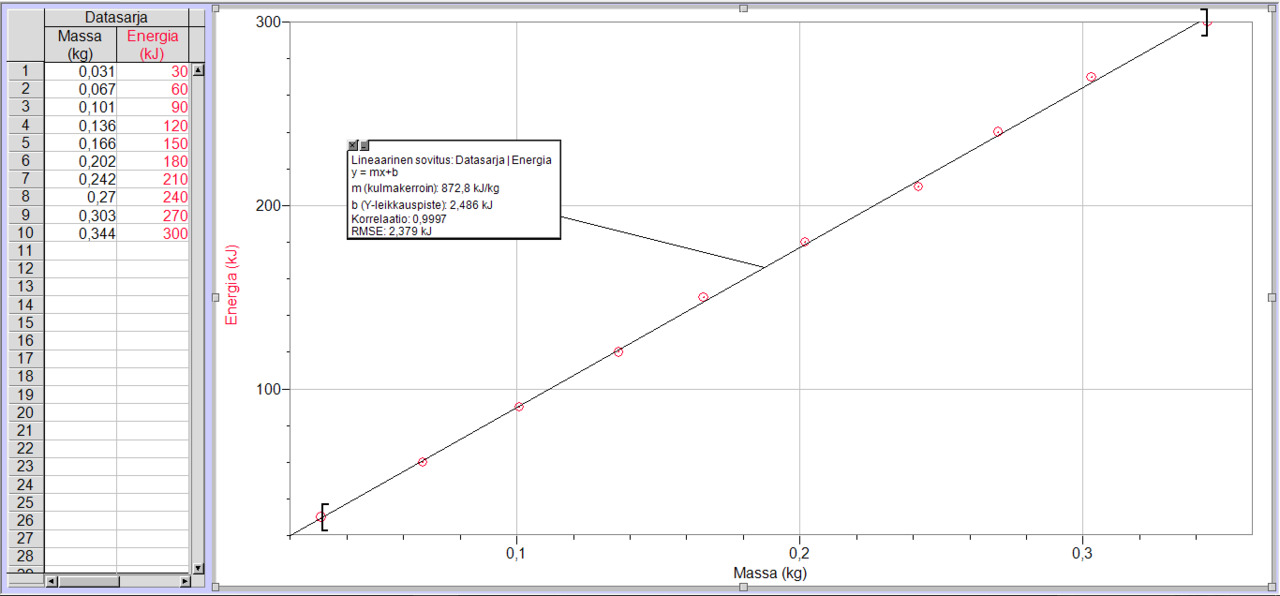
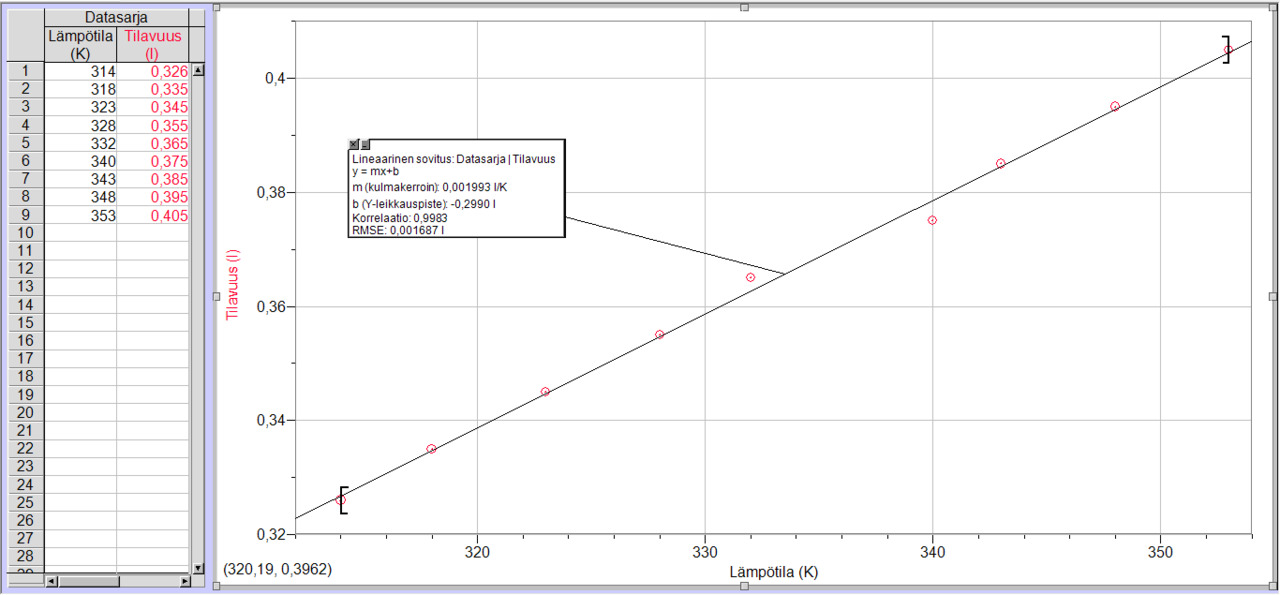
FY2S

S.121 13-7

Logger-pro:n mukaan etanolin ominaishöyrystymislämpö on 872,8kJ/kg

S.121 13-4

a)
$Q=sm=333\frac{kJ}{kg}\cdot0{,}15kg=49{,}95\approx50kJ$
b)
$Q=rm=6800\frac{kJ}{kg}\cdot0{,}012kg=81{,}6\approx82kJ$

S.121 13-2

$Q=sm=64\frac{kJ}{\left(kg\right)}\cdot30{,}0kg=1920kJ$
$1920kJ:58\cdot100=3310{,}344828\approx3300kJ$

S.121 13-1

a)
Veden haihuminen iholta sitoo energiaa.
b)
Kynsilakanpoistoaineen haihtuminen iholta sitoo energiaa.
c)

Pullon lämpötila on korkeampi kuin kylmäpyyhe
Veden haihtuminen märkäpyyheltä sitoo energiaa, ja se ottaa pullolta sitä energiaa.

S.113 12-4

a)
1. T<273,15K
2. 273,15K<T<373,15K
3. 373,15K<T<647,4K
4. T>647,4K
b)
p>0,00061Mpa
c)
1. Jähmentyy
2. Tiivistyy
d)
Höyry

S.113 12-3

a)
Olonmuodon muutoksessa lämpötila ei muutu
b)
Silloin kun pullo on vielä jääkaapissa, jääkaapissa oleva kastepiste on veden jäähtymispistettä alempi, sen seurauksena vesihöyry härmistyy kylmille pullon pinnalle kuuraksi.
Kun sitä otetaan pois jääkaapista, Sen ympäröivä lämpötila on korkeampi kuin aikasemmin, siitä seuraa kuuran sulaminen vesipisaraksi.

S.113 12-2

a)
Kiinteä, neste ja kaasu
b)
1. Sublimoituminen
2. Sulaminen
3. Höyrystyminen
c)
Aine A:lla on matalampi sulamispiste kuin B:llä

S.113 12-1

a) B
b) B
c) A
d) B

S.101 11-7

$T_1=25°C=298{,}15K$

$p_1=102{,}1kPa=102{,}1\cdot10^3Pa$

$T_2=-18°C=255{,}15K$

Vakiotilavuudessa muutos noudattaa Gay-lussacian lakia.

$\frac{p_1}{T_1}=\frac{p_2}{T_2}\ <=>p_2=\frac{p_1T_2}{T_1}$

$p_2=\frac{102{,}1\cdot10^3Pa\cdot255{,}15K}{298{,}15K}=87374{,}8616Pa$

Pullon korkkiin aiheuttaa voima sisä- ja ulkopuolinen paine-ero.

Oletetaan, että lkopuolella on normaali ilmanpaine $P_0=102{,}1\cdot10^3Pa$ , Joten voiman aiheuttaa paine on $p=p_0-p_2=102{,}1\cdot10^3Pa-87374{,}8616Pa=13925{,}138Pa$
$p=\frac{F}{A\ }<=>F=pA$

$A=4{,}3cm^2=0.00043m^2$

$F=13925{,}138Pa\cdot0{,}00043m^2=5{,}9878N\approx6{,}0N$

S.101 11-3

$T_1=22°C=295{,}15K$

$V_1=2{,}0l=2{,}0dm^3$

$V_2=2{,}0dm^3\cdot1{,}25=2{,}5dm^3$

Muutos noudattaa Charlesin lakia, jolloin

$\frac{V_1}{T_1}=\frac{V_2}{T_2}<=>V_1T_2=V_2T_1$

$T_2=\frac{V_2T_1}{V_1}=\frac{2{,}5dm^3\cdot295{,}15K}{2{,}0dm^3}=368{,}9375K$

$\Delta T=T_2-T_1=368{,}9375K-295{,}15K=73{,}7875K\approx74°C$

S.101 11-2

a) Että ne ovat suoraan verrannollisia.
b) Pisteet eivät ovat täsmälleen kuvaajalla.

S.101 11-1

$V_1=250dm^3$

$p_1=220kPa=220\cdot10^3Pa$

$V_2=150dm^3$

Muutos naudattaa Boylen lakia, jolloin

$p_1V_1=p_2V_2<=>p_2=\frac{p_1V_1}{V_2}$

$p_2=\frac{220\cdot10^3Pa\cdot250dm^3}{150dm^3}=366666{,}6667\approx370kPa$

S.93 10-8

$V_1=40dm^3=0{,}04m^3$

$p_1=10{,}0MPa=10{,}0\cdot10^6Pa$
$p_0=101{,}3kpa=101325Pa$
$T_1=17°C=17°C\ +273{,}15=290{,}15K$

$\rho_{NTP}=1{,}43\frac{mol}{dm^3}$
$T_{NTP}=273{,}15K$

Lasketaan mikä olisi kyseisen kaasun tilavuus normaaliolosuhteissa. Kun kaasu määrä ei muutu, sen massa pysyy vakiona

$\frac{p_1V_1}{T_1}=\frac{p_{NTP}V_{NTP}}{T_{NTP}}$

, jolloin

$p_1V_1T_{NTP}=p_{NTP}V_{NTP}T_1$

$V_{NTP}=\frac{p_1V_1T_{NTP}}{T_1p_{NTP}}$
$V_{NTP}=\frac{10{,}0\cdot10^6Pa\cdot40{,}0dm^3\cdot273{,}15K}{290{,}15K\cdot101325Pa}=3716{,}3962dm^3$

Tiheydelle on

$\rho_{NTP}=\frac{m}{V_{NTP}}$

eli massa on

$m=\rho_{NTP}\cdot V_{NTP}$
$=1{,}43\frac{g}{dm^3}\cdot3716{,}3962dm^3$
$=5314{,}447g$
$\approx5{,}3kg$

S.93 10-7

$V_1=1{,}5l=0{,}0015m^3$
$V_2=1{,}5l=0{,}0015m^3$
$p_1=101{,}3kPa$
$p_2=x$
$t_1=25°C=25°C\ +273{,}15=298{,}15K$
$t_2=-25°C=-25°C+273{,}15=248{,}15K$
$\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$ , jolloin $p_1V_1T_2=p_2V_2T_1$

Jolloin

$p_2=\frac{p_1V_1T_2}{V_2T_1}=\frac{101{,}3kpa\cdot0{,}0015m^3\cdot248{,}15K}{0{,}0015m^3\cdot298{,}15K}=84{,}31...\approx84kPa$

S.93 10-6

$V_1=75cm^3=75\cdot10^{-6}m^3$
$V_2=33cm^3=33\cdot10^{-6}m^3$
$p_1=101{,}3kPa$
$p_2=x$
$t_1=18°C=18°C\ +273{,}15=291{,}15K$
$t_2=37°C=37°C+273{,}15=310{,}15K$
$\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$ , jolloin $p_1V_1T_2=p_2V_2T_1$

Jolloin

$p_2=\frac{p_1V_1T_2}{V_2T_1}=\frac{101{,}3kpa\cdot75\cdot10^{-6}m^3\cdot310{,}15K}{33\cdot10^{-6}m^3\cdot291{,}15K}=245{,}2515...\approx245{,}3kPa=0{,}25mPa$

S.93 10-5

$n=\frac{m}{M}$

n= Aine määrä (mol)

m= Massa (g)

M= Moolimassa (g/mol)

$m\left(H_2\right)=12g$
$M\left(H_2\right)=1{,}008\frac{g}{mol}\cdot2=2{,}016\frac{g}{mol}$

$n=\frac{m}{M}=\frac{12g}{2{,}016\frac{g}{mol}}=5{,}9523...\approx6{,}0mol$

$n=\frac{N}{N_A}\ <=>\ N=nN_A$
$N\left(H_2\right)=5{,}952mol\cdot6{,}022\cdot10^{23}=3{,}584\cdot10^{24}\approx3{,}6\cdot10^{24}$

S.85 9-7

a)

$m_v=0{,}50kg$

$m_j=0{,}30kg$
$t_v=42°C$
$t_j=0°C$

$c_v=4{,}19\frac{kj}{\left(kg\cdot K\right)}$

$\Delta T_v=42K$

Veden luovuttama energia on:

$Q_v=c_vm_v\Delta T_v$

$=4{,}19\frac{kj}{\left(kg\cdot K\right)}\cdot0{,}50kg\cdot42K=87{,}99\approx88kj$

$Q_j=0{,}30kg\cdot333\frac{kj}{kg}=99{,}9kj$

Siis veden luovuttama energia ei riitä jään sulattamiseen, jolloin lopputuloksena on veden ja jään seos ja lämpötila on 0°C

S.86 9-5

$m_v=25kg$
$\Delta T_1=18K$

$\Delta T_2=6K$

$c_v=4{,}1819\frac{kj}{\left(kg\cdot K\right)}=4181{,}9\ \frac{j}{\left(kg\cdot K\right)}$

$m_v=\frac{c_vm_v\Delta T_2}{c_v\Delta T_1}=\frac{4{,}1819\frac{kj}{\left(kg\cdot K\right)}\cdot25kg\cdot6K}{4{,}1819\frac{kj}{\left(kg\cdot K\right)}\cdot18K}=8{,}333...\approx8kg$

S.86 9-2

b), d)

S.77 8-8

$\Delta l=\alpha l_0\Delta T$

$t_1=20°C$

$t_2=95°C$

$\alpha=20{,}8\cdot10^{-6}\frac{1}{K}$

$\Delta t=t_2-t_1=95°C-20°C=75°C$
$\Delta T=75K$

$\Delta l=20{,}8\cdot10^{-6}\frac{1}{K}\cdot65{,}00mm\cdot75K=0{,}1014\approx0{,}10mm$

S.77 8-6

a)

$\Delta l=\alpha l_0\Delta T$

$t_1=-12{,}0°C$

$t_0=+78{,}0°C$

$\alpha=16{,}8\cdot10^{-6}\frac{1}{K}$

$\Delta t=t_2-t_1=90°C$
$\Delta T=90K$

$\Delta l=16.8\cdot10^{-6}\frac{1}{K}\cdot912mm\cdot90K=1{,}378944mm$

$l=l_0+\Delta l=912mm+1{,}378944mm=913{,}378944\approx913mm$

b)

$\Delta l=\alpha l_0\Delta T$

$t_1=+18{,}0°C$

$t_0=-25°C$

$\alpha=11{,}7\cdot10^{-6}\frac{1}{K}$

$\Delta t=t_2-t_1=-43°C$
$\Delta T=-43K$

$\Delta l=11{,}7\cdot10^{-6}\frac{1}{K}\cdot20000mm\cdot\left(-43K\right)=-10{,}062mm=-1{,}0062cm\approx-1cm$

v: Lyhenee noin 1cm.

S.77 8-4

a) Kahdesta eri tavalla laajenevasta metallista tehty liuska. Liuskat on liitetty toisiinsa kiinni niin, että ne pystyvät vapaasti laajenemaan. Tämä saa aikaan sen, että lämpötilan muutos muuttaa liuskan muotoa. Kaksoismetalli taipuu lämmetessään eri suuntaan kuin jäähtyessään.
b) Ylöspäin

S.77 8-2

S.65 7-6

a)
1
b)
3
c)
3
d)
4

S.65 7-4

$Q_1=Q_2+W$

S.65 7-3

Turven lämpöarvo:

$11H=11\ \frac{MJ}{kg}=11MJ\cdot35000kg=385000MJ=385000000000J$

$P=\frac{W}{t}=\frac{385000000000J}{\left(24\cdot60\cdot60\right)s}=4456018{,}519W$

$4456018{,}519W\cdot43\%=1916087{,}963W\approx1{,}9MW$

S.65 7-2

$\eta_{\max}=\frac{T_1-T_2}{T_1}=1-\frac{T_2}{T_1}=1-\frac{\left(25°C+273{,}15\right)K}{\left(540°C+273{,}15\right)K}=0{,}633...\approx0{,}63=63\%$

S.48 5-11

Kyllä
Kuljettaminen: Kuuman kattilan kautta lämpö siirtyy vedelle.
Joutuminen: Kattila lämpenee kuuman lieden vaikutuksesta.
Lämpösäteily: Kattila ja kuuma vesi säteilevät ympäristöään.

S.48 5-10

a)
Kuuma vesi tulee vesiputken kautta patteriin ja siitä se patteri lämpenee.
b)
Veden kuumentaessa vesimolekyylien liike nopeutuu ja sen sisäenergia kasvaa. Kun se on kiertänyt jonkin aikaa patterissä, sen sisäenergiaa heikenee, ja energia siirtyy lämmön muodossa ympäristöön.

S.48 5-8

a)
Paksu ihonalainen eristävä rasvakerros suojaa kylmältä mervedeltä. Eli se estää lämmön pääsemistä hylkeen kehon ulkopuolelle.
b)
Että siihen väliin pääsee ilma, ja ilma on hyvä lämmön eriste.
c)
Paksu karvapeite eristä lämpöä tehokammin.

S.47 5-2

a) Joutuminen
b) Lämpösäteily
c) Kuljettuminen

S.41 4-9

a)
$\eta=\frac{E_{tuotto}}{E_{otto}}=\frac{21W}{54W}=0{,}3888...\approx0{,}39=39\%$
b)
$E_{hukka-\%}=\frac{E_{otto}-E_{tuotto}}{E_{tuotto}}=\frac{54W-21W}{54W}=0{,}6111...\approx0{,}61=61\%$

S.41 4-4

a)
$W=Fs=mg\Delta h=5{,}0kg\cdot9{,}81\frac{m}{s}\cdot0{,}95m=46{,}5975J\approx47J$
b)
$W=Fs=mg\Delta h=5{,}0kg\cdot9{,}81\frac{m}{s}\cdot0m=0J$
c)
$W=Fs=mg\Delta h=5{,}0kg\cdot9{,}81\frac{m}{s}\cdot5m=245{,}25J\approx250J$

S.41 4-3

a)
$W=Fs=25N\cdot150m=3750J\approx3{,}8kJ$
b)
Työntävä voima F, kitka ja ilmavastus

S.41 4-2

a)
Työntävä voima F, kitka ja ilmavastus
Painovoima ja ilmavastus
b)
Kitka, ilmavastus

S.41 4-1

Kitka
b)
Jarruttaessa auton mekaaninen energia heikenee kitkan takia, ja heikentyneen energia vapautuu lämpönä.

S.33 3-8

a)
$120\frac{km}{h}:3{,}6=33{,}3333....\approx33{,}333\frac{m}{s}$

$E_k=\frac{1}{2}mv^2=\frac{1}{2}\cdot1300kg\cdot\left(33{,}333\frac{m}{s}\right)^2=722207{,}7779\approx720000J=720kJ$
b)

$50\frac{km}{h}:3{,}6=13{,}8888\approx13{,}889\frac{m}{s}$

$40\frac{km}{h}:3{,}6=11{,}1111\approx11{,}111\frac{m}{s}$

$E_k=\frac{1}{2}mv^2=\frac{1}{2}\cdot1300kg\cdot\left(13{,}889\frac{m}{s}\right)^2=125387{,}8087J$

$E_k=\frac{1}{2}mv^2=\frac{1}{2}\cdot1300kg\cdot\left(11{,}111\frac{m}{s}\right)^2=80245{,}30865J$

$\frac{125387{,}8087J-80245{,}30865J}{125387{,}8087J}=0{,}36002...\approx0{,}36=36\%$
Auto hidastuu

S.33 3-7

a)
$E_p=mgh$
$E_p=77kg\cdot9{,}81\frac{m}{s^2}\cdot10{,}9m=8233{,}533J\approx8200J=8{,}2kJ$
b)
$E_p=mgh$
$E_p=77kg\cdot9{,}81\frac{m}{s^2}\cdot0m=0J$
c)
$0J-8{,}2kJ=-8{,}2kJ$
d)
$E_k=\frac{1}{2}mv^2=\frac{1}{2}\cdot77kg\cdot\left(14\frac{m}{s}\right)^2=7546J\approx7500J=7{,}5kJ$

S.33 3-6

a) Ei voi, koska mikä niistä kertoimesta ei voi olla negatiivinen. (massa, putoamiskiihtyvyys, etäisyys)
b) Ei voi, koska liikessa vapauttaa energiaa riippumatta sen nopeudesta (hidastuva liike, kiihtyvä liike)

S.21 2-6

a)
$A=18{,}4cm\cdot23{,}9cm=439{,}76cm^2=0{,}043976m^2$

$m=330g=0{,}33kg$

$g=9{,}81\frac{m}{s^2}$

$p=\frac{F}{A}=\frac{G}{A}=\frac{mg}{A}=\frac{0{,}33kg\cdot9{,}81\frac{m}{s^2}}{0{,}043976m^2}=73{,}615...\approx74Pa$
V: N. 74Pa.
b)
$p=\frac{F}{A}=101325Pa=\frac{F}{0{,}043976m^2}=101325Pa\cdot0{,}043976m^2=4455{,}8682N\approx4500N=4{,}5kN$
V: N.4,5kN.
c)
Kirjan alhalta tuleva ilmapaine kumoa ylähltä tuleva ilmapainetta

S.21 2-3

a)
$A=180mm\cdot530mm=95400mm^2=0{,}0954m^2$

$m=68kg$

$g=9{,}81\frac{m}{s^2}$

$p=\frac{F}{A}=\frac{G}{A}=\frac{mg}{A}=\frac{68kg\cdot9{,}81\frac{m}{s^2}}{0{,}0954m^2}=6992{,}45283Pa\approx7000Pa=7{,}0kPa$
V: 7,0kPa.
b)
$A=210cm^2=0{,}021m^2$

$m=68kg$

$g=9{,}81\frac{m}{s^2}$

$p=\frac{F}{A}=\frac{G}{A}=\frac{mg}{A}=\frac{68kg\cdot9{,}81\frac{m}{s^2}}{0{,}021m^2}=31765{,}71429\approx32000Pa=32kPa$
V: 32kPa.

S.15 1-9

a)
$T=\left(t+273{,}15\right)K=36{,}5°C+273{,}15=309{,}65K$
b)
$T=\left(t+273{,}15\right)K=-18°C+273{,}15=255{,}15K$
c)
$t=\left(T-273{,}15\right)°C=90K-273{,}15=-183.15°C$

S.15 1-4

a) Paine p, tilavuus V ja lämpötila T
b) Ravistelussa samppanjapullon paine ja lämpötila kasvavat.

S.15 1-3

a) Eristetty (Lähes)
b) Suljettu
c) Avoin