Esimerkki 3 malliratkaisu
a) Paikka on esitetty graafisesti ajan funktiona alla.
b) Putoamisliikettä voidaan mallintaa tasaisesti kiihtyvänä liikkeenä, jossa paikan yleinen lauseke on
[[$ x=x_0+v_0 t +\frac{1}{2}at^2 $]]
Lähdettäessä levosta kohdasta nolla lauseke on
[[$ x=\frac{1}{2}at^2 $]]
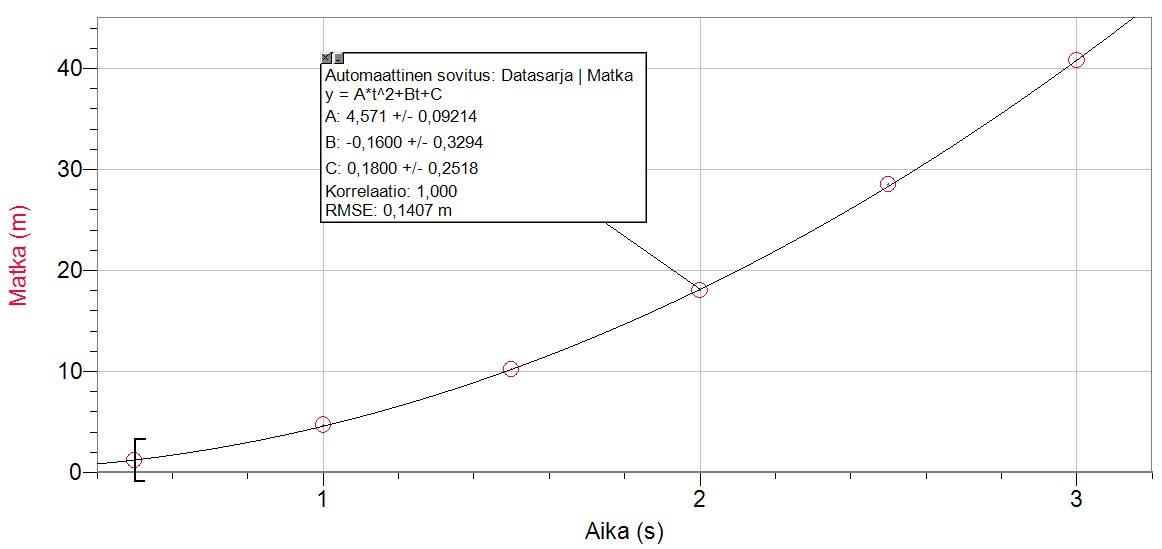
Paikan kuvaajaa voidaan siis mallintaa paraabelilla. Kun pistejoukkoon sovitetaan paraabeli, saadaan mittausohjelmistolla sen toisen asteen termin kertoimeksi 4,571 (m/s2) (Kuva alla). Paikan lausekkeessa tämä kerroin on puolet kiihtyvyydestä, eli
[[$ \frac{1}{2}a=4,571 \text { m/s}^2 $]].
Putoamiskiihtyvyys on siis mittauksen perusteella
[[$ a=2\cdot 4,571 \dfrac{\text{m}}{\text{s}^2}\approx 9,1 \dfrac{\text{m}}{\text{s}^2} $]]
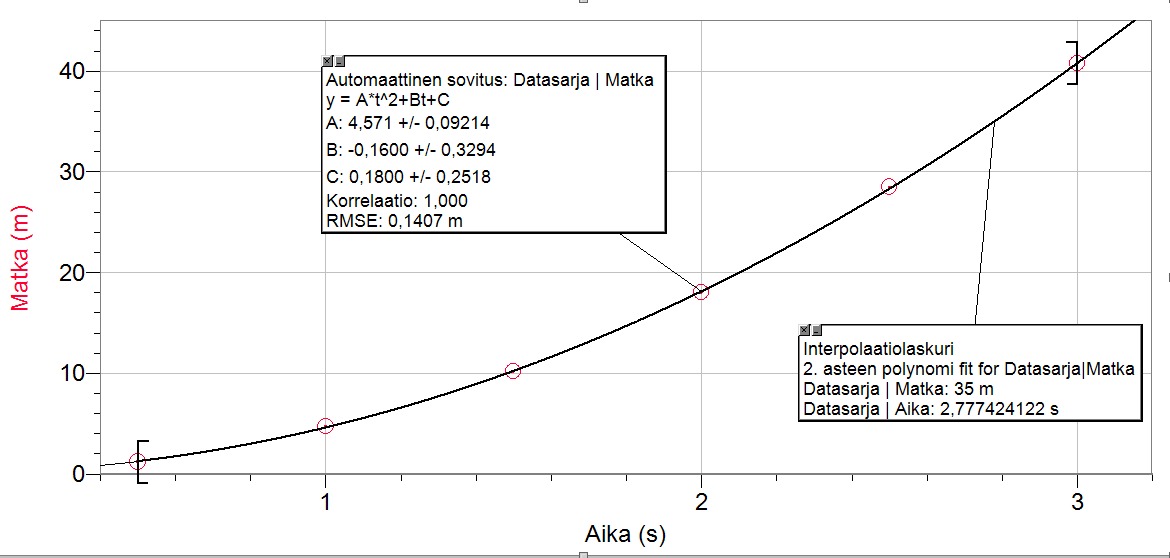
c) Mittausohjelmiston interpolointitoiminnolla voidaan määrittää ajanhetki, jolloin metka on 35 m. Alla olevan kuvaajan mukaan aika on noin 2,8 s.


b) Putoamisliikettä voidaan mallintaa tasaisesti kiihtyvänä liikkeenä, jossa paikan yleinen lauseke on
[[$ x=x_0+v_0 t +\frac{1}{2}at^2 $]]
Lähdettäessä levosta kohdasta nolla lauseke on
[[$ x=\frac{1}{2}at^2 $]]
Paikan kuvaajaa voidaan siis mallintaa paraabelilla. Kun pistejoukkoon sovitetaan paraabeli, saadaan mittausohjelmistolla sen toisen asteen termin kertoimeksi 4,571 (m/s2) (Kuva alla). Paikan lausekkeessa tämä kerroin on puolet kiihtyvyydestä, eli
[[$ \frac{1}{2}a=4,571 \text { m/s}^2 $]].
Putoamiskiihtyvyys on siis mittauksen perusteella
[[$ a=2\cdot 4,571 \dfrac{\text{m}}{\text{s}^2}\approx 9,1 \dfrac{\text{m}}{\text{s}^2} $]]

c) Mittausohjelmiston interpolointitoiminnolla voidaan määrittää ajanhetki, jolloin metka on 35 m. Alla olevan kuvaajan mukaan aika on noin 2,8 s.
