1.2 Apuvälineet fysiikan kokeessa
Laskinohjelmistot
Taulukko ja koejärjestelmän ohjeet
Lisäksi koejärjestelmän ohjeet sisältävät fysiikan taulukoita ja kaavoja. Koejärjestelmän ohje ei ole yhtä laaja kuin digitaulukko, esimerkiksi isotooppitaulukko puuttuu. Koejärjestelmän ohjeet ovat selainversiona osoitteessa https://cheat.abitti.fi/build/index.html?fi
Kaavaeditori
Ratkaisuihin kuuluvat matemaattiset lausekkeet kirjoitetaan Abittijärjestelmässä vastauskentän kaavaeditorilla. Kaavaeditori on upotettuna vastauskenttään. Vastauksen voi tehdä myös laskinohjelmistoilla ja niistä otetuilla kuvakaappauksilla.
Kaavaeditori on helppokäyttöinen. Editori tuottaa LaTeX-ladontajärjestelmän mukaan koodattuja lausekkeita. Lausekkeet voidaan kirjoittaa editorin pikanäppäinten tai Latex-komentojen avulla. Latex-komentoja ei ole välttämätöntä tuntea, mutta joidenkin komentojen tunteminen nopeuttaa lausekkeiden kirjoittamista.
| Merkki | Kaava | Esimerkki käytöstä | Esikatselu |
|---|---|---|---|
| Kertolasku | \cdot | m cdot a | [[$ m \cdot a $]] |
| Murtoluku | \dfrac{}{} | \dfrac{\Delta v}{\Delta t} | [[$ \dfrac{\Delta v}{\Delta t} $]] |
| Alaindeksi | _ | v_0 | [[$ v_0 $]] |
| Yläindeksi | ^ | 2,0 \text{ m/s}^2 | [[$ 2,0 \text{ m/s}^2 $]] |
| Summa | \sum | \sum \bar{F}=\bar{0} | [[$ \sum \bar{F}=\bar{0} $]] |
| Likiarvo | \approx | F \approx 45 \text{ N} | [[$ F \approx 45 \text{ N} $]] |
| Yläviiva | \bar | \bar{F} | [[$ \bar{F} $]] |
| μ | \mu | F_\mu | [[$ F_\mu $]] |
| α | \alpha | \tan \alpha = \mu | [[$ \tan \alpha = \mu $]] |
| Δ | \Delta | \Delta t | [[$ \Delta t $]] |
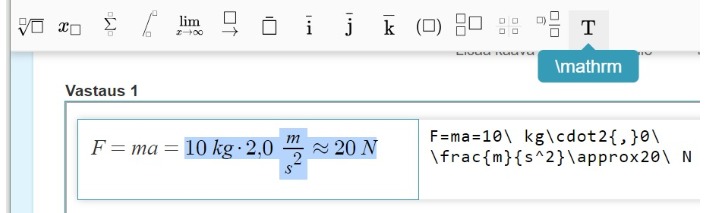
Kaavaeditori tuottaa kaavat matemaatisena tekstinä. Suureiden yksiköt kirjoitetaan ei-kursiivilla, jotta ne erottuvat suuretunnuksista. Matemaattiset komentojen tekeminen normaalilla fontilla onnistuu \mathrm -komennolla. Tämä on hyödyllinen esimerkiksi yksikössä [[$\mathrm{m/s^2}$]]. Tällöin voidaan korottaa edelleen toiseen potenssiin, mutta teksti on normaalilla fontilla. Komento \text tekee normaalia fonttia, eikä se tunne komentoja, kuten komentoa potenssiin korottamista. Matemaattinen teksti on kursiivia. Se voi poistaa \mathrm-pikanäppäimellä (kts. kuva).
Laskenta suureyhtälöillä ohjelmistoja apuna käyttäen
Yhtälöitä ja yhtälöryhmiä voi ratkaista symbolisen laskennan ohjelmistojen tai symbolisen laskimen avulla (CAS-laskin). Ohjelmistoja käyttämällä voi ratkaista tehtävän tai tarkistaa vastauksen. Ohjelmistojen oikeanlainen käyttö säästää aikaa monimutkaisessa tehtävässä. Laskennallisessa tehtävässä ratkaistaan lauseke tuntemattomalle suureelle eli pelkkä numeerinen ratkaisu ei riitä täysiin pisteisiin.
Ohjelmiston käyttö osana vastausta
- Tilannetta kuvaavat yhtälöt esitetään yleisessä muodossa ja perusteltuna.
- Mainitaan, että ohjelmistoa hyödynnetään ratkaisussa ja liitetään mielellään kuvankaappaus ohjelmistosta.
- Ilmoitetaan ohjelmiston antama ratkaistu lauseke.
Alla ovat esimerkit yhtälön ratkaisusta sekä yhtälöparin ratkaisusta GeoGebran CAS-laskin ohjelmistolla.
Yhtälön ratkaisu GeoGebralla
Tarkastellaan tilannetta, jossa kappale on tasaisesti kiihtyvässä liikkeessä. Kappale lähtee liikkeelle levosta. Kappalen kiihtyvyys on [[$2{,}5 \ \mathrm{m/s^2}$]] ja kulkema matka [[$28 \ \mathrm{m}$]]. Taulukkokirjasta saadaan kaava paikalle tasaisesti kiihtyvässä liikkeessä.
Paikka tasaisesti kiihtyvässä liikkeessä
[[$ x=\dfrac{1}{2}at^2 $]]
Ratkaistaan yhtälöstä aika [[$t$]] GeoGebran CAS -ympäristössä. GeoGebra ratkaisee yhtälön muuttujan [[$t$]] suhteen ja antaa vastauksen. Vastauksen muoto noudattaa matemaattista esitystapaa, jossa nimittäjässä ei esiinny neliöjuuressa olevaa lauseketta. Käsin laskemalla päädytään usein muotoon [[$ t=\sqrt{\dfrac{2x}{a}} $]]. Vaikka lausekkeet näyttävät erilaisilta, ovat samat. GeoGebra antaa ratkaisuksi ajalle myös negatiivisen lausekkeen. Fysiikassa negatiiivinen ratkaisu on epämielekäs tulos, eikä sitä tarvitse huomioida, jos se on itsestään selvää.
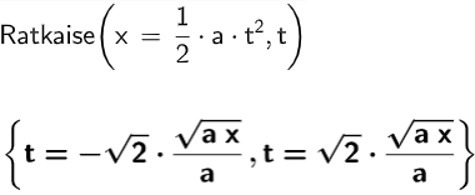
Kun ratkaisu kirjoitetaan GeoGebran CAS-laskimessa huomioi seuraavat asiat.
- Desimaalierotin on piste. Pilkkua käytetään komentojen sisällä osien erotteluun. Luku puoli (1/2) kirjoitetaan GeoGebrassa muotoon 0.5, EI MUODOSSA 0,5.
- Kahden muuttujan tulo kirjoitetaan aina kertomerkkiä käyttäen tai muuttujien väliin kirjoiteaan välilyönti. Ajan ja nopeuden tulo kirjoitetaan muodossa "v*t" tai "v t", EI MUODOSSA "vt". Yhteenkirjoitettuna "vt" tarkoitta GeoGebrassa suuretta, jonka tunnus on [[$vt$]].
GeoGebralla voi ratkaista liikkeeseen kuluvan ajan suuruuden sijoita komennolla. Komennon avulla aukeaa taulukko, johon lähtöarvot sijoitetaan. Lukuarvot sijoitetaan desimaalipistettä käyttäen. Noin merkistä painamalla saadaan desimaalimuotoinen vastaus. Vastauksen tarkkuus määrätään asetuksista. Vastauksen tarkkuuden voi valita desimaalien tai merkitsevien numeroiden mukaan.

Taulukko ei kelpaa suureiden suuruuksien perusteluiksi, vaan lukuarvot on kirjoitettava erikseen vastaukseen.
[[$a=2{,}5 \ \mathrm{m/s^2}$]]
[[$x=28 \ \mathrm{m}$]]
[[$t=4{,}7333 \ \mathrm{s}\approx 4{,}7 \ \mathrm{s}$]]
Yhtälöryhmän ratkaisu GeoGebralla
Ratkaistaan aika ja kiihtyvyys tasaisesti kiihtyvän liikkeen yleisistä yhtälöistä[[$ s=v_0 t+\dfrac{1}{2}at^2 $]] ja [[$ v=v_0+at $]].
Yhtälöryhmä tai yhtälöpari ratkaistaan Ratkaise-komennolla siten, että yhtälöt sekä muuttujat sijoitetaan aaltosulkeiden sisään ja erotetaan toisistaan pilkulla. Lukuarvon laskeminen tehdään samalla tavalla kuin yhden yhtälön tapauksessa edellä tehtiin.
Kuvioiden piirtäminen
Voimakuviot
Voimakuviota voi piirtää millä tahansa piirto-ohjelmistolla. Voimakuviossa voimat piirretään suorina viivoina ja nuolina. Voimanuolet päättyvät voiman vaikutuspisteeseen tai alkavat vaikutuspisteestä. Voimat nimetään kuviossa suureiden tunnuksina. Suureiden tunnukset kirjoitetaan vektorimuodossa. Voimat nimetään kuvion yhtyeteen, jotta on selvää mitä mikäkin tunnus tarkoittaa. Voimakuvioita piirtää kätevästi Abitissa TI-Nspiren Fysiikan piirto -ohjelmalla.
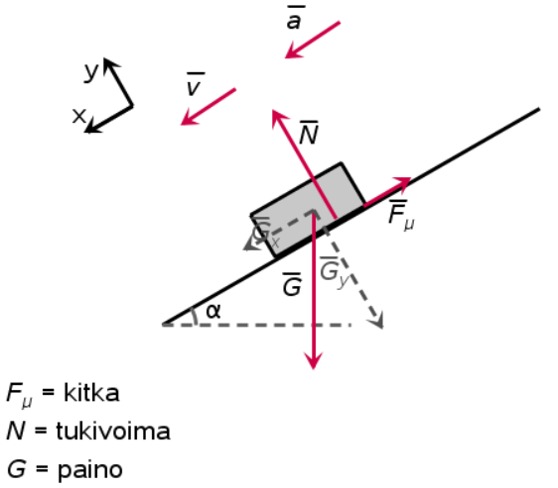
Kuvassa on TI-Nspiren Fysiikan piirto -sovelluksella piirretty voimakuvio. Piirto-ohjelmassa saa valmiina oletuksena kaltevan tason, kappaleen, [[$(x,y)$]]-suunnan merkinnän, vektorien jaon komponentteihin ja voimien nimeämisen. Voimakuvioon merkitään kiihtyvyyden suunta, jos kappale on kiihtyvässä liikkeessä ja nopeuden suunta, jos kappale on liikkeessä. Voimakuviossa voimien komponentteihin jako ei ole välttämätön, mutta jos se tehdään, on komponentit piirrettävä erilaisilla nuolilla kuin varsinaiset voimat. Kuviossa voimien komponentit ovat katkoviivanuolia.
Kytkentäkaaviot
Kytkentäkaaviot tehdään kytkentäkaaviomerkkejä käyttäen. Kytkentäkaavioiden yhteyteen nimetään komponentit niiden tunnuksilla ja merkitään tarvittaessa sähkövirtojen suunnat. Kytkentäkaavioita piirtää kätevästi TI-Nspiren Fysiikan piirto -ohjelmalla.
Kuvassa on TI-Nspiren Fysiikan piirto -sovelluksella piirretty kytkentäkaavio. Tyypillisimmät kytkentäkaaviomerkit saadaan ohjelmassa pikanäppäimin ja komponenttien nimeäminen on yksinkertaista.
Tilannekuvat
Tilannekuvia voi tarvita fysiikan tehtävissä havainnollistamaan vastausta. Tilannekuviota voi piirtää vapaasti millä tahansa ohjelmalla. Kuviot kannattaa piirtää yksinkertaisina, eikä kuvioiden näyttävyydellä ole merkitystä. Tärkeintä on, että kuvio havainnollistaa ilmiötä. TI-Nspiren Fysiikan piirto -ohjelmassa on valittavana valmiita tilannekuva pohjia, joita voi täydentää vastaukseen sopivalla tavalla. Valittavana on esimerkiksi sähkö- ja magneettikenttiä, aaltoliikkeeseen liittyviä tilannekuvia tai valmiita merkkejä varauksille ja hiukkasille.
Kuvassa on TI-Nspiren Fysiikan piirto -sovelluksella piirretty havainnollistava kuva aaltorintaman taittumisesta. Aaltorintaman taittumiselle on oma pohjakuva, jota on täydennetty kulmasymbolein. Taittumisen suuntaa voidaan muuttaa pikanäppäimin.