Kpl.10
10-3
a) Painonnostokilpailussa painoja on helpompi nostaa, jos painot ovat yhtä suuret ja tangon eri päissä. Painopiste on tangon geometrisessä keskipisteessä. Painonnostaja pyrkii asettamaan kätensä yhtä kauas tangon painopisteestä (geometrisestä keskipisteestä).
b) Painonnostossa käytetään leveää otetta, jolloin tanko on mahdollisimman helppo pitää tasapainossa. Raskaat levyt tangon päissä aiheuttavat suuren momentin tankoon. Jos kädet olisivat lähekkäin, pienikin ero käsien ja tangon keskipisteen välisissä etäisyyksissä aiheuttaisi suuren eron vasempaan ja oikeaan käteen kohdistuvissa voimissa. Samoin pienikin tangon kiertoliike tangon keskipisteen ympäri noston aikana olisi vaikea pysäyttää, nostaja menettäisi helposti tasapainonsa sivusuunnassa.
10-4
Joidenkin kukkien, esimerkiksi tulppaanien, varsi kasvaa nopeasti maljakossa. Samalla maljakon pohjalla oleva vesi vähenee sen noustessa varteen. Kukat voivat taipua kasvaessaan kauas reunan yli, ja kukkaasetelman painopiste muuttuu. Maljakon, veden ja kukkien yhteinen painopiste voi siirtyä maljakon kapean pohjan tukipinnan ulkopuolelle, varsinkin jos kukat taipuvat samaan suuntaan. Näin maljakko voi kaatua itsestään.
10-7
Tasapaksuun hirteen kohdistuva paino vaikuttaa hirren painopisteeseen eli keskipisteeseen. Hirren tasapainoehto pystysuunnassa on eli
eli  . Kun suunta ylös on positiivinen, saadaan skalaariyhtälö
. Kun suunta ylös on positiivinen, saadaan skalaariyhtälö  .
.
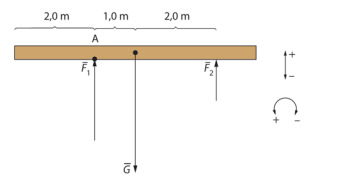
Vasemmanpuoleisen tukivoiman vaikutuskohta on A. Valitaan kohta A momenttiakseliksi. Kun kiertosuunta vastapäivään on positiivinen, akselin A suhteen momenttiyhtälö on
vaikutuskohta on A. Valitaan kohta A momenttiakseliksi. Kun kiertosuunta vastapäivään on positiivinen, akselin A suhteen momenttiyhtälö on 
Tukivoiman suuruus on
suuruus on

Tukivoman suuruus saadaan yhtälöstä
suuruus saadaan yhtälöstä  , joten
, joten 
Voimat ovat 460N ja 920N
10-9



 : Väijerin jännitysvoima
: Väijerin jännitysvoima
 : Painovoima
: Painovoima
 : Saranan tukivoima
: Saranan tukivoima



















![F=\sqrt[]{F_x^2+F_y^2}=\sqrt[]{382{,}59^2+765{,}18^2}=855{,}49...\approx860N](https://math-demo.abitti.fi/math.svg?latex=F%3D%5Csqrt%5B%5D%7BF_x%5E2%2BF_y%5E2%7D%3D%5Csqrt%5B%5D%7B382%7B%2C%7D59%5E2%2B765%7B%2C%7D18%5E2%7D%3D855%7B%2C%7D49...%5Capprox860N)


10-11

Lankun alapäässä vaikuttavat lattian tukivoima ja kitka
ja kitka  . Yläpäässä lankkuun kohdistuu seinän tukivoima
. Yläpäässä lankkuun kohdistuu seinän tukivoima ja koska seinä oletettiin liukkaaksi, kitka
ja koska seinä oletettiin liukkaaksi, kitka . Lankun painopisteessä vaikuttaa lankkuun kohdistuva paino
. Lankun painopisteessä vaikuttaa lankkuun kohdistuva paino 
Tasapainoehto vaakasuunnassa on Newtonin II lain perusteella eli
eli  . Kun suunta oikealle on positiivinen, skalaariyhtälöstä
. Kun suunta oikealle on positiivinen, skalaariyhtälöstä  saadaan
saadaan 
Asetetaan momenttiakseli pisteeseen A. Kun kiertosuunta vastapäivään on positiivinen, tasapainotilanteessa momenttien summa akselin A suhteen on eli
eli  .Koska
.Koska 
momenttiehto saadaan muotoon
saadaan muotoon  eli
eli  ,
,
josta saadaan .
.
Toisaakta suorakulmaisen kolmion trigonometrian perusteella on
 , joten yhtälöstä
, joten yhtälöstä

saadaan kulma
a) Painonnostokilpailussa painoja on helpompi nostaa, jos painot ovat yhtä suuret ja tangon eri päissä. Painopiste on tangon geometrisessä keskipisteessä. Painonnostaja pyrkii asettamaan kätensä yhtä kauas tangon painopisteestä (geometrisestä keskipisteestä).
b) Painonnostossa käytetään leveää otetta, jolloin tanko on mahdollisimman helppo pitää tasapainossa. Raskaat levyt tangon päissä aiheuttavat suuren momentin tankoon. Jos kädet olisivat lähekkäin, pienikin ero käsien ja tangon keskipisteen välisissä etäisyyksissä aiheuttaisi suuren eron vasempaan ja oikeaan käteen kohdistuvissa voimissa. Samoin pienikin tangon kiertoliike tangon keskipisteen ympäri noston aikana olisi vaikea pysäyttää, nostaja menettäisi helposti tasapainonsa sivusuunnassa.
10-4
Joidenkin kukkien, esimerkiksi tulppaanien, varsi kasvaa nopeasti maljakossa. Samalla maljakon pohjalla oleva vesi vähenee sen noustessa varteen. Kukat voivat taipua kasvaessaan kauas reunan yli, ja kukkaasetelman painopiste muuttuu. Maljakon, veden ja kukkien yhteinen painopiste voi siirtyä maljakon kapean pohjan tukipinnan ulkopuolelle, varsinkin jos kukat taipuvat samaan suuntaan. Näin maljakko voi kaatua itsestään.
10-7
Tasapaksuun hirteen kohdistuva paino vaikuttaa hirren painopisteeseen eli keskipisteeseen. Hirren tasapainoehto pystysuunnassa on

Vasemmanpuoleisen tukivoiman
Tukivoiman
Tukivoman
Voimat ovat 460N ja 920N
10-9
Tasapainoehto etenemisen suhteen x-suunnassa
Tasapainoehto etenemisen suhteen y-suunnassa
Tasapainoehto pyörimisen suhteen
a)
b)
Voiman suunta
10-11

Lankun alapäässä vaikuttavat lattian tukivoima
Tasapainoehto etenemisen suhteen pystysuunnassa on Newtonin II lain perusteella  eli
eli  . Kun suunta ylös on positiivinen, skalaariyhtälöstä
. Kun suunta ylös on positiivinen, skalaariyhtälöstä  saadaan
saadaan  .
.
Tasapainoehto vaakasuunnassa on Newtonin II lain perusteella
Asetetaan momenttiakseli pisteeseen A. Kun kiertosuunta vastapäivään on positiivinen, tasapainotilanteessa momenttien summa akselin A suhteen on
momenttiehto
josta saadaan
Toisaakta suorakulmaisen kolmion trigonometrian perusteella on
saadaan kulma