1. Tasainen liike
Tasainen liike
Tasainen liike
Tasainen liike tarkoittaa liikettä, jossa liikkeen suunta ja nopeus säilyvät samana. Arkielämässä törmätään harvoin tilanteisiin, joissa liike olisi tasaista. Koulumatkalla pyörällä tai bussilla kuljettaessa joudutaan vaihtamaan suuntaa koko ajan ja jarruttamaan sekä kiihdyttämään vauhtia.
 Urheiluauto on tasaisessa liikkeessä sen ajaessa suoraa tietä tasaista nopeutta.
Urheiluauto on tasaisessa liikkeessä sen ajaessa suoraa tietä tasaista nopeutta.
Jos auto ajaa piikkisuoraa tietä koko ajan täsmälleen samalla nopeudella, niin silloin auto on tasaisessa liikkeessä. Kun auto on tasaisessa liikkeessä, niin sen kyydissä olevan matkustajan on vaikea sanoa liikkuko auto vai ei, jos matkustaja laittaa silmänsä kiinni.
 Auton nopeusmittari näyttää auton hetkellisen nopeuden.
Auton nopeusmittari näyttää auton hetkellisen nopeuden.
Vaikka liike ei olisikaan tasaista, niin nopeutta, jolla siirrytään paikasta toiseen, voidaan kuvata keskinopeudella. Keskinopeuteen vaikuttavat kuljetun matkan pituus ja matkaan käytetty aika. Mitä lyhyemmässä ajassa matka taitetaan, niin sitä suurempi on keskinopeus.
Nopeuden tunnus on v (engl. velocity). Nopeuden yksikkönä käytetään fysiikassa metriä sekunnissa ([[$\frac{m}{s}$]]) ja arkielämässä usein kilometriä tunnissa ([[$\frac{km}{h}$]]). Jos keskinopeus automatkalla Kotkasta Helsinkiin on 80 [[$\frac{km}{h}$]], niin yhden tunnin aikana kuljetaan keskimäärin 80 kilometrin matka jarruttelusta ja kiihdyttelystä huolimatta.
Keskinopeuden laskeminen
Kuten sanottu, niin keskinopeuteen v vaikuttavat kuljettu matka s (space) ja matkaan käytetty aika t (time). Keskinopeus lasketaan matkan ja ajan avulla kaavalla [[$$keskinopeus=\frac{matka}{aika}$$]] eli [[$$v=\frac{s}{t}.$$]]
Yksikön muunnoksia
Tuulen nopeus ilmaistaan säätiedotuksissa metreinä sekunnissa, mutta kuinka paljon on esimerkiksi 20 metriä sekunnissa kilometreinä tunnissa?
Luodaan muunnoskaava, jolla metrit sekunnissa voidaan muuttaa kilometreiksi tunnissa ja toisinpäin:
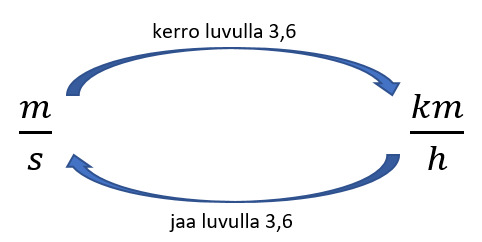
Oikeastaan tarvitsee vain ilmaista kilometri metreinä ja tunti sekunteina. Yksi kilometri on 1000 metriä ja yksi tunti on [[$60 \cdot 60=3600$]] sekuntia, joten
[[$$1 \ \frac{m}{s}=3600 \ \frac{m}{h}=3,6 \ \frac{km}{h}$$]] ja [[$$ 1 \ \frac{km}{h}=1000 \ \frac{m}{h}=\frac{1000}{3600} \ \frac{km}{h}=\frac{1}{3,6} \ \frac{km}{h}. $$]]
Tasainen liike koordinaatistossa
Liikettä on usein hyvä esittää aika-matka-koordinaatistossa. Tällöin selviää helposti muun muassa mikä on ollut liikkeen nopeus kullakin ajanhetkellä ja kuinka paljon koko matkaan on kulunut aikaa. Huomaa, että tasaisen liikeen kuvaaja on aina suora aika-matka-koordinaatistossa!
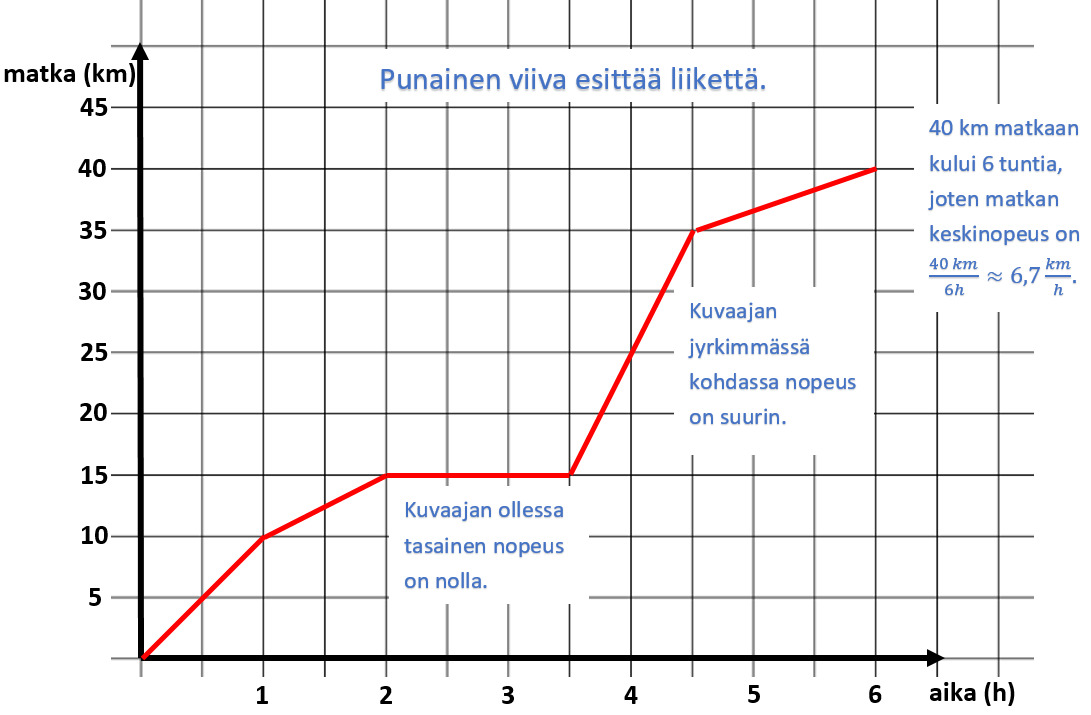 Yllä olevasta kuvaajasta nähdään muun muassa, että ensimmäisen tunnin aikana kuljettiin 10 km matka ja toisen tunnin aikana 5 km matka. Sen jälkeen liike pysähtyi 1,5 tunnin ajaksi, minkä jälkeen kuljettiin tunti nopeudella 20 km/h ja viimeisen tunnin aikana kuljettiin 5 km matka.
Yllä olevasta kuvaajasta nähdään muun muassa, että ensimmäisen tunnin aikana kuljettiin 10 km matka ja toisen tunnin aikana 5 km matka. Sen jälkeen liike pysähtyi 1,5 tunnin ajaksi, minkä jälkeen kuljettiin tunti nopeudella 20 km/h ja viimeisen tunnin aikana kuljettiin 5 km matka.
Tasainen liike tarkoittaa liikettä, jossa liikkeen suunta ja nopeus säilyvät samana. Arkielämässä törmätään harvoin tilanteisiin, joissa liike olisi tasaista. Koulumatkalla pyörällä tai bussilla kuljettaessa joudutaan vaihtamaan suuntaa koko ajan ja jarruttamaan sekä kiihdyttämään vauhtia.
 Urheiluauto on tasaisessa liikkeessä sen ajaessa suoraa tietä tasaista nopeutta.
Urheiluauto on tasaisessa liikkeessä sen ajaessa suoraa tietä tasaista nopeutta. Jos auto ajaa piikkisuoraa tietä koko ajan täsmälleen samalla nopeudella, niin silloin auto on tasaisessa liikkeessä. Kun auto on tasaisessa liikkeessä, niin sen kyydissä olevan matkustajan on vaikea sanoa liikkuko auto vai ei, jos matkustaja laittaa silmänsä kiinni.
 Auton nopeusmittari näyttää auton hetkellisen nopeuden.
Auton nopeusmittari näyttää auton hetkellisen nopeuden. Vaikka liike ei olisikaan tasaista, niin nopeutta, jolla siirrytään paikasta toiseen, voidaan kuvata keskinopeudella. Keskinopeuteen vaikuttavat kuljetun matkan pituus ja matkaan käytetty aika. Mitä lyhyemmässä ajassa matka taitetaan, niin sitä suurempi on keskinopeus.
Nopeuden tunnus on v (engl. velocity). Nopeuden yksikkönä käytetään fysiikassa metriä sekunnissa ([[$\frac{m}{s}$]]) ja arkielämässä usein kilometriä tunnissa ([[$\frac{km}{h}$]]). Jos keskinopeus automatkalla Kotkasta Helsinkiin on 80 [[$\frac{km}{h}$]], niin yhden tunnin aikana kuljetaan keskimäärin 80 kilometrin matka jarruttelusta ja kiihdyttelystä huolimatta.
Keskinopeuden laskeminen
Kuten sanottu, niin keskinopeuteen v vaikuttavat kuljettu matka s (space) ja matkaan käytetty aika t (time). Keskinopeus lasketaan matkan ja ajan avulla kaavalla [[$$keskinopeus=\frac{matka}{aika}$$]] eli [[$$v=\frac{s}{t}.$$]]
| Esimerkki Automatka Kotkasta Kouvolaan kestää [[$45$]] minuuttia. Kouvolaan on matkaa [[$60$]] kilometriä. Laske matkan keskinopeus. Listataan annetut suureet: Matka [[$s=60 \ km$]] Aika [[$t=45 \ min=0,75 \ h$]] Keskinopeus v saadaan jakamalla kuljettu matka s siihen käytetyllä ajalla t eli [[$$v=\frac{s}{t}=\frac{60 \ km}{0,75 \ h}=80 \ \frac{km}{h}.$$]] |
Yksikön muunnoksia
Tuulen nopeus ilmaistaan säätiedotuksissa metreinä sekunnissa, mutta kuinka paljon on esimerkiksi 20 metriä sekunnissa kilometreinä tunnissa?
Luodaan muunnoskaava, jolla metrit sekunnissa voidaan muuttaa kilometreiksi tunnissa ja toisinpäin:
Oikeastaan tarvitsee vain ilmaista kilometri metreinä ja tunti sekunteina. Yksi kilometri on 1000 metriä ja yksi tunti on [[$60 \cdot 60=3600$]] sekuntia, joten
[[$$1 \ \frac{m}{s}=3600 \ \frac{m}{h}=3,6 \ \frac{km}{h}$$]] ja [[$$ 1 \ \frac{km}{h}=1000 \ \frac{m}{h}=\frac{1000}{3600} \ \frac{km}{h}=\frac{1}{3,6} \ \frac{km}{h}. $$]]

Tasainen liike koordinaatistossa
Liikettä on usein hyvä esittää aika-matka-koordinaatistossa. Tällöin selviää helposti muun muassa mikä on ollut liikkeen nopeus kullakin ajanhetkellä ja kuinka paljon koko matkaan on kulunut aikaa. Huomaa, että tasaisen liikeen kuvaaja on aina suora aika-matka-koordinaatistossa!
 Yllä olevasta kuvaajasta nähdään muun muassa, että ensimmäisen tunnin aikana kuljettiin 10 km matka ja toisen tunnin aikana 5 km matka. Sen jälkeen liike pysähtyi 1,5 tunnin ajaksi, minkä jälkeen kuljettiin tunti nopeudella 20 km/h ja viimeisen tunnin aikana kuljettiin 5 km matka.
Yllä olevasta kuvaajasta nähdään muun muassa, että ensimmäisen tunnin aikana kuljettiin 10 km matka ja toisen tunnin aikana 5 km matka. Sen jälkeen liike pysähtyi 1,5 tunnin ajaksi, minkä jälkeen kuljettiin tunti nopeudella 20 km/h ja viimeisen tunnin aikana kuljettiin 5 km matka.