Kahden muuttujan epäyhtälö
Kahden muuttujan yhtälöllä on ääretön määrä ratkaisuja.
Esimerkiksi
Suoran yhtälön y = 2x + 4 toteuttavat esimerkiksi pisteiden (0, 4), (1, 6) ja (1,7 ; 7,4) koordinaatit, mutta myös ääretön määrä muita.
Suoran yhtälön ratkaisut muodostavat koordinaatistossa suoran.
Yhtälön y = 2x2 toteuttavat esimerkiksi pisteiden (−2, 8), (−1, 2), (0,0), (1, 2) ja (2, 8) koordinaatit, mutta myös ääretön määrä muita.
Jos pisteet merkitään koordinaatistoon, muodostuu paraabeli.
Jos kyseessä on kuitenkin epäyhtälö, ratkaisua ei voi esittää koordinaatistossa viivana vaan ratkaisuna on jokin alue koordinaatistossa.
Harjoitus
Tutki täällä, miltä epäyhtälöiden ja yhtälöiden ratkaisut näyttävät koordinaatistossa.
Kahden muuttujan epäyhtälön ratkaisu esitetään usein piirroksena koordinaatistossa. Kyseessä on jokin alue koordinaatistossa, joten ensin pitää selvittää alueen raja. Sen jälkeen voidaan päätellä, kumpi puoli rajasta on oikea puoli ja esimerkiksi värittää oikea alue koordinaatistossa.
Esimerkiksi
Esitä epäyhtälön 6x − 2y < 4 ratkaisu koordinaatistossa.
Aloitetaan selvittämällä, mikä on alueen raja. Ratkaistaan ensin epäyhtälö y:n suhteen. (Muista pitää epäyhtälö epäyhtälönä.)
6x − 2y < 4 , josta siirretään x-termi oikealle
−2y < − 6x + 4 , josta jakamalla y:n kertoimella saadaan
y > 3x − 2
(huomaa, että epäyhtälön merkki kääntyi, koska jaettiin negatiivisella luvulla)
Alueen rajana toimii siis suora y = 3x − 2. Epäyhtälömuodosta nähdään, että ratkaisuna on alue, jossa y on suurempi kuin suora eli ratkaisuna on suoran yläpuolinen alue.
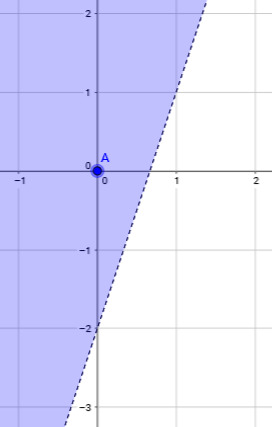
Tämä voidaan vielä varmistaa sijoittamalla alueella olevan pisteen koordinaatit alkuperäiseen epäyhtälöön. Esimerkiksi piste (0, 0) on selvästi halutulla alueella. Sijoitetaan sen koordinaatit alkuperäiseen epäyhtälöön.
6x − 2y < 4 ja piste (0, 0)
6 ∙ 0 − 2 ∙ 0 < 4
0 < 4, joka pitää paikkansa eli piste toteuttaa epäyhtälön. Vaikuttaa siltä, että ratkaisu on piirretty oikein.
Kuvassa raja on piirretty katkoviivalla, koska alkuperäinen epäyhtälö sisältää aidon epäyhtäsuuruuden ( < ). Viivalla olevat pisteet kuten esimerkiksi (0, −2) eivät toteuta epäyhtälöä.
Viivalla olevan pisteen koordinaateilla saadaan 6 ∙ 0 − 2 ∙ (−2) < 4 eli 4 < 4, mikä ei pidä paikkaansa.
Jos epäyhtälö sisältäisi yhtäsuuruuden ( < ), viivalla olevat pisteet olisivat osa ratkaisua.
Katso myös esimerkkivideo Sotungin matikka -kanavalta.
Harjoitus
Piirrä seuraavien epäyhtälöiden ratkaisut koordinaatistoon. Voit tarkastaa ratkaisut Geogebrassa.
a) y < 4x − 4
b) 2x + 4y > 8
c) 6 + 2y < 7x
Esimerkiksi
Suoran yhtälön y = 2x + 4 toteuttavat esimerkiksi pisteiden (0, 4), (1, 6) ja (1,7 ; 7,4) koordinaatit, mutta myös ääretön määrä muita.
Suoran yhtälön ratkaisut muodostavat koordinaatistossa suoran.
Yhtälön y = 2x2 toteuttavat esimerkiksi pisteiden (−2, 8), (−1, 2), (0,0), (1, 2) ja (2, 8) koordinaatit, mutta myös ääretön määrä muita.
Jos pisteet merkitään koordinaatistoon, muodostuu paraabeli.
Jos kyseessä on kuitenkin epäyhtälö, ratkaisua ei voi esittää koordinaatistossa viivana vaan ratkaisuna on jokin alue koordinaatistossa.
Harjoitus
Tutki täällä, miltä epäyhtälöiden ja yhtälöiden ratkaisut näyttävät koordinaatistossa.
Kahden muuttujan epäyhtälön ratkaisu esitetään usein piirroksena koordinaatistossa. Kyseessä on jokin alue koordinaatistossa, joten ensin pitää selvittää alueen raja. Sen jälkeen voidaan päätellä, kumpi puoli rajasta on oikea puoli ja esimerkiksi värittää oikea alue koordinaatistossa.
Esimerkiksi
Esitä epäyhtälön 6x − 2y < 4 ratkaisu koordinaatistossa.
Aloitetaan selvittämällä, mikä on alueen raja. Ratkaistaan ensin epäyhtälö y:n suhteen. (Muista pitää epäyhtälö epäyhtälönä.)
6x − 2y < 4 , josta siirretään x-termi oikealle
−2y < − 6x + 4 , josta jakamalla y:n kertoimella saadaan
y > 3x − 2
(huomaa, että epäyhtälön merkki kääntyi, koska jaettiin negatiivisella luvulla)
Alueen rajana toimii siis suora y = 3x − 2. Epäyhtälömuodosta nähdään, että ratkaisuna on alue, jossa y on suurempi kuin suora eli ratkaisuna on suoran yläpuolinen alue.

Tämä voidaan vielä varmistaa sijoittamalla alueella olevan pisteen koordinaatit alkuperäiseen epäyhtälöön. Esimerkiksi piste (0, 0) on selvästi halutulla alueella. Sijoitetaan sen koordinaatit alkuperäiseen epäyhtälöön.
6x − 2y < 4 ja piste (0, 0)
6 ∙ 0 − 2 ∙ 0 < 4
0 < 4, joka pitää paikkansa eli piste toteuttaa epäyhtälön. Vaikuttaa siltä, että ratkaisu on piirretty oikein.
Kuvassa raja on piirretty katkoviivalla, koska alkuperäinen epäyhtälö sisältää aidon epäyhtäsuuruuden ( < ). Viivalla olevat pisteet kuten esimerkiksi (0, −2) eivät toteuta epäyhtälöä.
Viivalla olevan pisteen koordinaateilla saadaan 6 ∙ 0 − 2 ∙ (−2) < 4 eli 4 < 4, mikä ei pidä paikkaansa.
Jos epäyhtälö sisältäisi yhtäsuuruuden ( < ), viivalla olevat pisteet olisivat osa ratkaisua.
Katso myös esimerkkivideo Sotungin matikka -kanavalta.
Harjoitus
Piirrä seuraavien epäyhtälöiden ratkaisut koordinaatistoon. Voit tarkastaa ratkaisut Geogebrassa.
a) y < 4x − 4
b) 2x + 4y > 8
c) 6 + 2y < 7x