2.2 Newtonin menetelmä

229
$x\approx-0{,}70347$

230

231
x=1.109956 or x=3.35302 or x=5.50089

232
a)
$x\approx2{,}0$
b)
$x\approx2{,}0$
c)
ei mikään

233

Annettu alkuarvo ei toimi, otetaan uudeksi alkuarvoksi luku 3

$x\approx2{,}76929$

Annettu alkuarvo ei toimi, otetaan uudeksi alkuarvoksi luku

$x\approx4{,}02752$

234
Funktio on kasvava eli sillä on korkeitaan yksi ratkaisu

Lasketaan funktion ratkaisut välin pätepisteessä 0 ja 1

jos tuloksien merkit vaihtuu, funktio noudataa Bolzanon lausetta, tällöin funktiolla on nollakohta avoimella välillä ]0,1[

$f\left(0\right)=-2$

$f\left(1\right)=1$

Kun alkuarvaus1, tulos on 0,83512, ei muita ratkaisuja.

235
a) 3

b) 5

236
$\approx-0{,}4425$

237

$\sin\left(x\right)+2x=3$

$\sin\left(x\right)+2x-3=0$

Merkitään

$f\left(x\right)=\sin x+2x-3$

Tutkitaan onko funktiolla f enemmän kuin yksi nollakohta

Funktio f on jatkuva kaikkialla

Tutkitaan funktion f kulkua deravaatan avulla

$f'\left(x\right)=\cos x+2$

Tiedetään, että

$-1\le\cos x\le1\ \parallel+2$

$1\le\cos x+2\le3$

Derivaattafunktio $f'\left(x\right)\ge1$ , jolloin funktio f on kasvava. Siten funktiolla f voi korkeintaan olla yksi nollakohta

Newtonin menetelmällä saatava likiarvo on siten funktion f ainoan nollakohdan likiarvo.

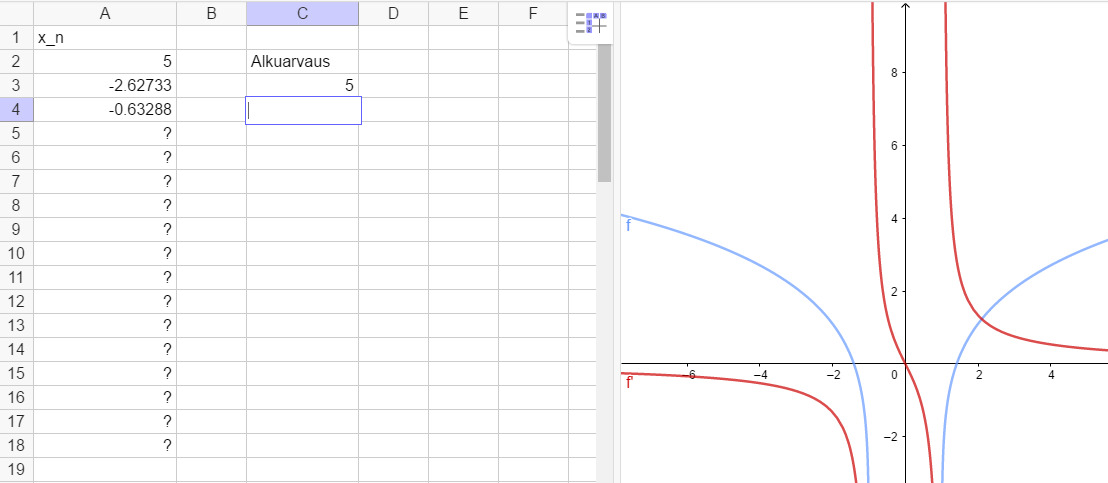
Newtonin menetelmän rekursiokaava

$x_{n+1}=x_n-\frac{f\left(x_n\right)}{f'\left(x_n\right)}$

Käytetään alkuarvoa

$x_1=1$

$x_2=x_1-\frac{f\left(x_1\right)}{f'\left(x_1\right)}=1-\frac{f\left(1\right)}{f'\left(1\right)}=1-\frac{\sin1+2\cdot1-3}{\cos1+2}=1{,}062405$

Lasketaan nollakohdalle likiarvot taulukkolaskentaohjelmalla

Nollakohta 5 desimaalin tarkkuudella on $x\approx1{,}06307$

Tarkistetaan, että näin on

Välillä ]1,063065;1,063075[ olevat luvut pyöristyvät 5 desimaalin tarkkuudella luvuksi 1,06307

$f\left(1{,}063065\right)<0$ ja

$f\left(1{,}063075\right)>0$

Bolzanon lauseen nojalla funktiolla on nollakohta kysesellä välillä ja se on $x\approx1{,}06307$

238
$x_0=2$ on funktion $2x^3-4x^2-8x+1$ derivaatan nollakohta

$x=0{,}1184$

$x=3{,}2009$

$x=-1{,}3193$

239

$e^x+ex$
yksi nollakohta

$x\approx-0{,}278465$

$\ln x-1$
yksi nollakohta

$x\approx2{,}718281$

241

$x\approx0{,}1612058$

$x\approx1{,}1418905$

242