4.1. Luottamusvälit
Virhemarginaali ja luottamusväli
Estimointi=otoksen avulla tehty arviointi.
Huolellisestikin tehdyssä estimoinnissa on yleensä virhettä eli poikkeamaa oikeista tuloksista.
Tietoa siitä, miten suuri virhe tietyllä todennäköisyydellä on kutsutaan virhemarginaaliksi.
Mitä suurempi otos, sitä pienempi virhemarginaali.
Virhemarginaalin avulla voidaan määrittää väli, jolla perusjoukon keskiarvo tietyllä todennäköisyydellä on. Tällaista väliä kutsutaan keskiarvon luottamusväliksi.
Virhemarginaalin suuruus riippuu siitä, kuinka suurella todennäköisyydellä eli luottamustasolla virheen yläraja halutaan tietää.
Huolellisestikin tehdyssä estimoinnissa on yleensä virhettä eli poikkeamaa oikeista tuloksista.
Tietoa siitä, miten suuri virhe tietyllä todennäköisyydellä on kutsutaan virhemarginaaliksi.
Mitä suurempi otos, sitä pienempi virhemarginaali.
Virhemarginaalin avulla voidaan määrittää väli, jolla perusjoukon keskiarvo tietyllä todennäköisyydellä on. Tällaista väliä kutsutaan keskiarvon luottamusväliksi.
Virhemarginaalin suuruus riippuu siitä, kuinka suurella todennäköisyydellä eli luottamustasolla virheen yläraja halutaan tietää.
Keskiarvon keskivirhe
Perusjoukon keskihajontaa ei yleensä tunneta, mutta sen tilalla voidaan käyttää otoksen keskihajontaa, jos otoskoko on yli 30.
Esim. Perusjoukon keskihajonta s=5,0 ja otoskoko 200. Laske keskiarvon keskivirhe.
\frac{5{,}0}{\sqrt{200}}\approx0{,}354
MAOL:sta löytyy seuraavia kaavoja
Perusjoukon odotusarvon \mu luottamusväli
![\left[\overline{x\ }\ -1{,}96\cdot\frac{s}{\sqrt{n}}{,}\ \ \overline{x}\ \ +1{,}96\cdot\frac{s}{\sqrt{n}}\ \right]\](https://math-demo.abitti.fi/math.svg?latex=%5Cleft%5B%5Coverline%7Bx%5C%20%7D%5C%20-1%7B%2C%7D96%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%7B%2C%7D%5C%20%5C%20%5Coverline%7Bx%7D%5C%20%5C%20%2B1%7B%2C%7D96%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%5C%20%5Cright%5D%5C%20)
95 %:n luottamusvälillä
![\left[\overline{x\ }\ -2{,}58\cdot\frac{s}{\sqrt{n}}{,}\ \ \overline{x}\ \ +2{,}58\cdot\frac{s}{\sqrt{n}}\ \right]\](https://math-demo.abitti.fi/math.svg?latex=%5Cleft%5B%5Coverline%7Bx%5C%20%7D%5C%20-2%7B%2C%7D58%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%7B%2C%7D%5C%20%5C%20%5Coverline%7Bx%7D%5C%20%5C%20%2B2%7B%2C%7D58%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%5C%20%5Cright%5D%5C%20)
99 %:n luottamusvälillä
![\left[\overline{x\ }\ -3{,}29\cdot\frac{s}{\sqrt{n}}{,}\ \ \overline{x}\ \ +3{,}29\cdot\frac{s}{\sqrt{n}}\ \right]\](https://math-demo.abitti.fi/math.svg?latex=%5Cleft%5B%5Coverline%7Bx%5C%20%7D%5C%20-3%7B%2C%7D29%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%7B%2C%7D%5C%20%5C%20%5Coverline%7Bx%7D%5C%20%5C%20%2B3%7B%2C%7D29%5Ccdot%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%5C%20%5Cright%5D%5C%20)
99,9 %:n luottamusvälillä
Suhteellisen osuuden luottamusväli
%7D%7Bn%7D%7D)
95 %:n luottamusvälillä99 %:n luottamusvälillä 99,9 %:n luottamusvälilläSuhteellisen osuuden luottamusväli
Esim. 2 sivu 88
Keskiarvon luottamusväli
Oppikirjan vimeo s.91
Kaavat löytyvät MAOL:sta hakusanalla "Luottamusväli"
Esim. 3 sivu 91 Z-estimaatti
Jos otos on suuri eli 
käytetään Z-estimaattia.
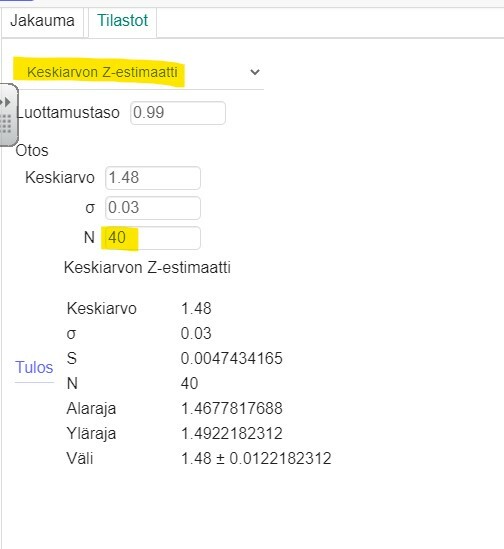
V:[ 1,46 ; 1,50 ] Muista oikea pyöristys!
Katso Video
käytetään Z-estimaattia.
V:[ 1,46 ; 1,50 ] Muista oikea pyöristys!
Katso Video
Esimerkki 4 s. 92
n<30 ota t-estimaatti
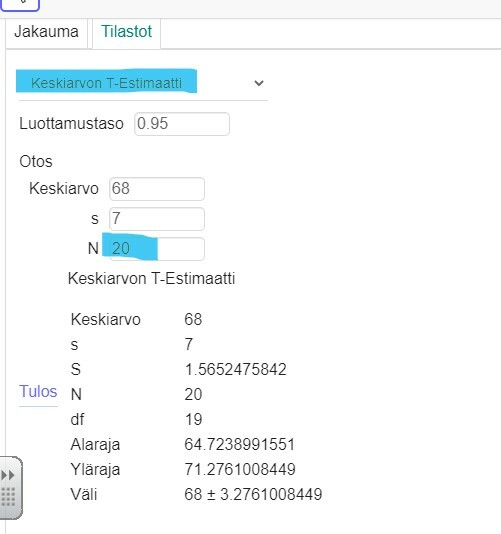
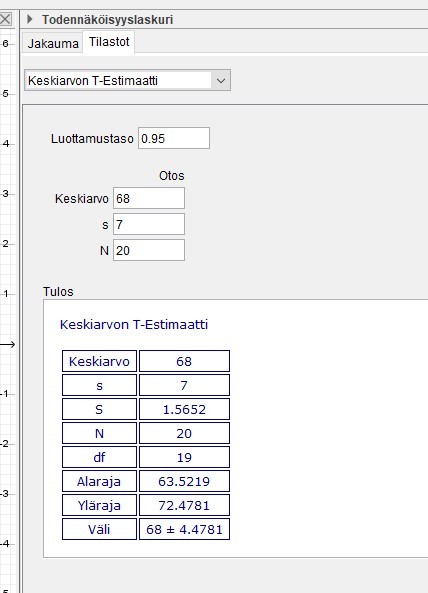
Videossa näytetään, miten t-jakaumaa noudattavan keskiarvon luottamusväli voidaan määrittää sopivalla ohjelmalla.
Klikkaa tästä.
Videossa näytetään, miten t-jakaumaa noudattavan keskiarvon luottamusväli voidaan määrittää sopivalla ohjelmalla.
Klikkaa tästä.
Esim. 4 sivu 92 Pieni otoskoko n < 30 Keskiarvon T-estimaatti
Suhteellisen osuuden luottamusväli
Esimerkki 5. s.93
Klikkaa tästä.
Videossa näytetään, miten suhteellisen osuuden luottamusväli voidaan määrittää sopivalla ohjelmalla.
Videossa näytetään, miten suhteellisen osuuden luottamusväli voidaan määrittää sopivalla ohjelmalla.