Esim.4.

Ratkaisu:
Kaikkien asiakkaiden lukumäärää ei tiedetä, valitaan Poisson jakauma

$\mu=6$

a) k=3

e= 2,71828182845904

e on vakio!
P(täsmälleen 3 asiakasta valittaa)= $\frac{6^3}{3!}e^{-6}=0{,}0892350783599$ $\approx8{,}9\ \%$

Laskettu SpeedCrunchilla:
(6^3)/3!*e^(-6)

= 0,0892350783599

V: $\approx8{,}9\ \%$

b)

P(alle 3 asiakasta valittaa)=P(täsmälleen nolla asiakasta valittaa)+P(täsmälleen yksi asiakas valittaa)+P(täsmälleen 2 asiakasta valittaa)
[Käytetty yhteenlaskusääntöä!] =0,00247...+ 0,0148...+0,0446...=0,061968804416658960 $\approx0{,}062=6{,}2\ \%$

SpeedCrunchilla laskettuna:

(6^0)/0!*e^(-6)+(6^1)/1!*e^(-6)+(6^2)/2!*e^(-6)

= 0,06196880441665896058

0,00247875217666635842+0,01487251305999815054+0,04461753917999445161

= 0,06196880441665896057 $\approx0{,}062=6{,}2\%$

V: 6,2 %

Geogebran todennäköisyyslaskurilla:

c)

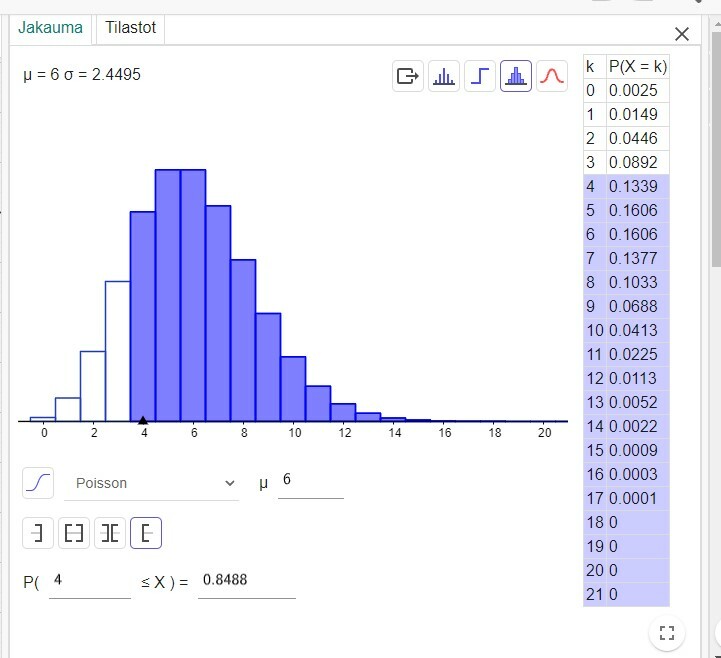
V: noin 84,9 %