The circumference and area of the circle
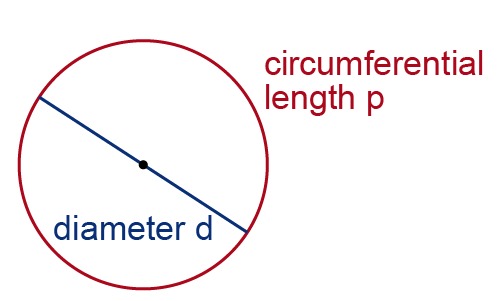
The ratio of a circle's circumferential length [[$ p $]] and diameter length [[$ d $]] is the same for all circles. The exact value in this respect is denoted by the Greek letter [[$ \ pi $]]
[[$$ \pi = \displaystyle\frac {p} {d} ≈ 3,1415926535... $$]][[$ \pi $]] (pronounced: "pi") is an infinite and non-periodic decimal number. When calculating the circumference of a circle or the area of a circle, a approximation of [[$ \pi $]] is usually used.
Since the length of a circle's diameter [[$ d$]] is twice the length of its radius [[$ r $]], the circumference length and area of a circle can be calculated if either the diameter or the radius of the circle is known.
The circumference of a circle
The circumference of a circle [[$ p $]] is the product of [[$ \pi $]] and the length of the diameter [[$ d $]]:
[[$$ p = \pi d = 2\pi r $$]]The area of a circle
The area [[$ A $]] of a circle is the product of [[$ \pi $]] and the radius [[$ r $]] squared:
[[$$ A = \pi r^2 $$]]Example 1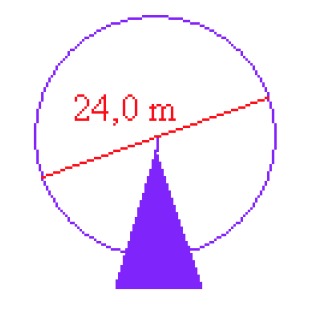
The diameter of a ferris wheel in an amusement park is 24.0 m. Calculate the distance traveled in one complete rotation of the ferris wheel by calculating the circumference of the ferris wheel.
[[$ p = \pi d ≈ 3,14 \cdot 24,0 $]] m [[$ = 75,4 $]] m
Answer: A distance of [[$ 75,4 $]] meters is traveled in one complete rotation of the ferris wheel.
Example 2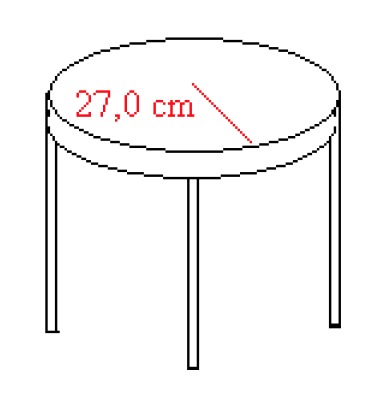
Calculate the area of a circular bedside table with a radius of 27.0 cm.
[[$ A = \pi r^2 ≈ \cdot $]] ([[$ 27,0 $]] cm)[[$ ^2 = 2289 $]] cm[[$ ^2 ≈ 2290 $]] cm[[$ ^2 $]]
Answer: The area of the bedside table is [[$ 2290 $]] cm[[$ ^2 $]] or [[$ 0,229 $]] m[[$ ^2 $]].