Let’s look at the powers of number two and the values of these powers.

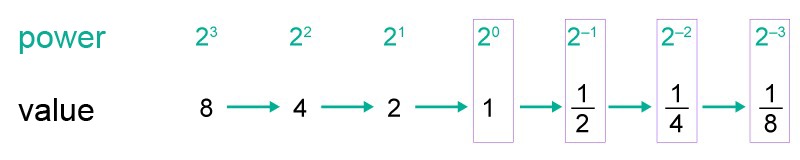
Going from right to left, the two exponents of the number decrease by one. The value of the power is calculated by dividing the value of the previous power by two. The same procedure can also be continued for the negative exponents.

When we compare the powers [[$ 2^3 $]] and [[$ 2^{-3} $]], we find that both powers have the value of eight. Correspondingly, if the exponent is [[$2$]] or [[$–2$]], the number [[$4$]] appears in the value. Marking the fractions [[$ \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8} $]] in form [[$ \dfrac{1}{2^1}, \dfrac{1}{2^2}, \dfrac{1}{2^3} $]], we see a clear connection with the corresponding positives.

The negative exponent of a power

The negative exponent of a power means the corresponding positive power of the base's reciprocal.

[[$ a^{-1} = \dfrac{1}{a} \qquad $]] and [[$ \qquad a^{-n} = \dfrac{1}{a^n} $]], when [[$ a \neq 0 $]]

Negative exponents are calculated according to the same calculation rules as positive exponents.

Examples

Example 1

Express the negative exponents as fractions.

a) [[$ 6^{-1} = \dfrac{1}{6^1} = \dfrac{1}{6} $]]

b) [[$ 4^{-3} = \dfrac{1}{4^3} = \dfrac{1}{64} $]]

c) [[$ \dfrac{3^2}{3^4} = 3^{2-4} = 3^{-2}=\dfrac{1}{3^2} = \dfrac{1}{9} $]]

Example 2

Express using negative exponents.

a)	[[$ \dfrac{1}{7} = 7^{-1} $]]
b)	[[$ \dfrac{1}{4^8} = 4^{-8} $]]
c)	[[$ \dfrac{1}{x^3} = x^{-3} $]]
d)	[[$ \dfrac{5x}{y^2} = 5xy^{-2} $]]
e)	[[$ \dfrac{1}{2a^4} = \dfrac{1}{2}a^{-4} $]]	Be careful with the base.