A polygon is regular if all of its sides are equal and all the angles are equal.

The most common regular polygons are equilateral triangles and squares.

Regular polygons can be drawn inside a circle in such a way that each of the polygon's vertices are located on the circle's circumference. Dividing the circle's full angle [[$360°$]] by the number of sides in the polygon gives the magnitude of the central angle corresponding to each of the polygon's sides.

Examples

Example 1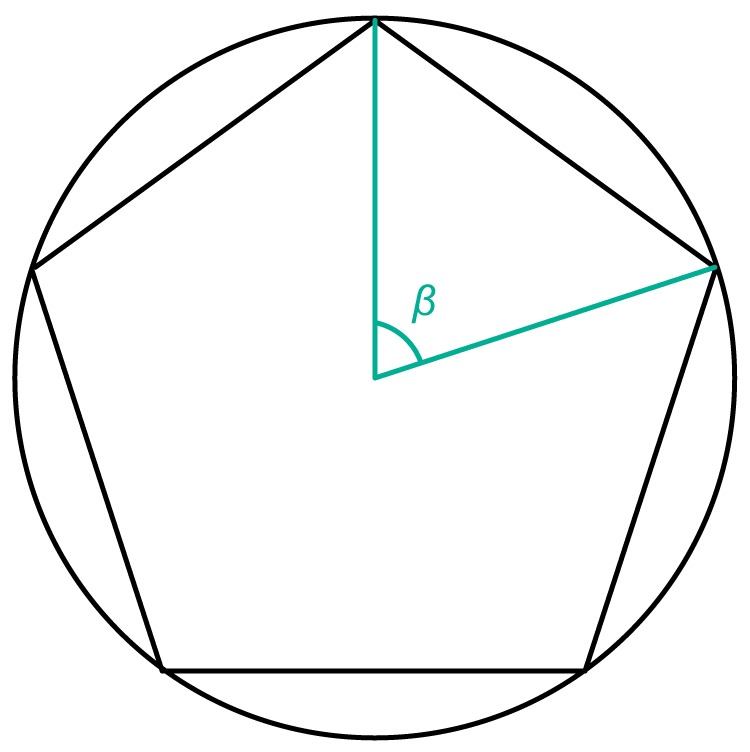

Calculate the magnitude of the central angle corresponding to the side of a regular pentagon.

When a regular pentagon is drawn inside a circle so that its vertices are on the circle's circumference, five sectors of equal size are formed. This can be seen in the adjacent figure. In this case, the central angle corresponding to the magnitude of each side is [[$ \beta = \dfrac{360°}{5} = 72° $]].

Example 2

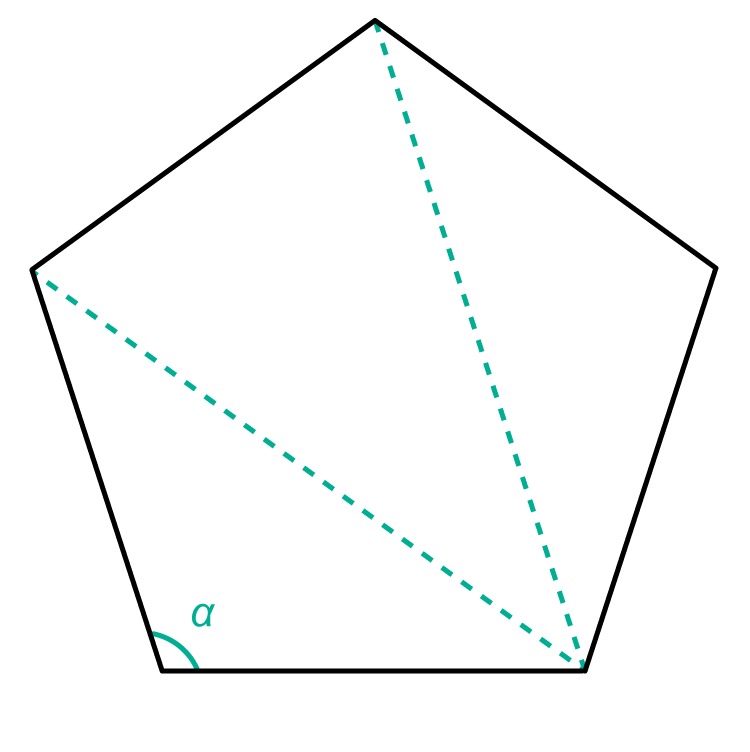Calculate the magnitude of the angle [[$ \alpha $]] of a regular pentagon.

A regular pentagon can be divided into three triangles. Since the sum of the angles of a triangle is always [[$ 180° $]], the sum of the angles of a regular pentagon is [[$3 \cdot 180° = 540° $]].

A regular pentagon has five angles of the same size, giving the magnitude of one angle [[$ \alpha = \dfrac{540°}{5} = 108°$]].

Example 3

Draw a regular hexagon.

Draw a circle with a radius equal to the side length of the hexagon.
Let P be a point on the perimeter.
Using a compass, separate six consecutive chords that are equal to the radius. Draw them by beginning from point P and following the circle's circumference .
Draw the chords that form the sides of the hexagon.