8. Polygons
Exercises
Polygons
When line segments are connected in succession so that the end point of the first segment becomes the starting point of the next segment, the result is a polygonal chain. If the start and end points of the polygonal chain converge, a closed polygonal chain is formed.

Definitions related to polygons
- A polygon is a part of a plane bounded by a closed, non-self-intersecting polygonal chain.
- The diagonal of a polygon connects two non-adjacent vertices.
- The angle of a polygon is the angle between two sides whose opening is inside the polygon.
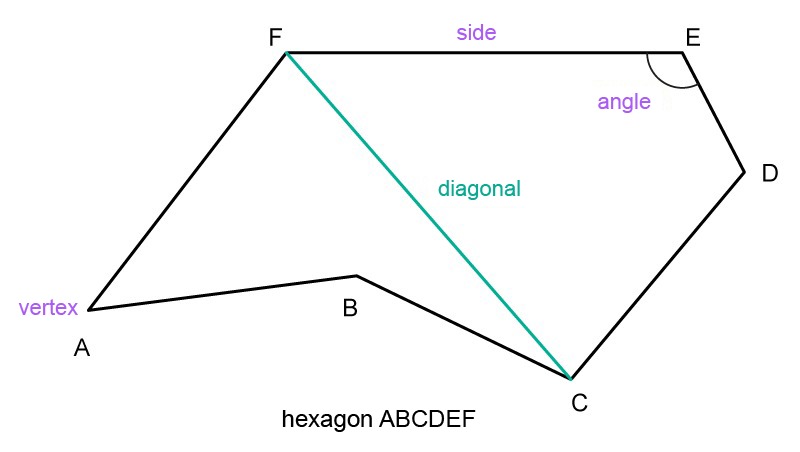
Polygons are named by listing the vertices of the polygon in order. A polygon can also be named by the number of vertices, angles, or sides in it. For example, a hexagon has 6 vertices, 6 angles, and 6 sides.
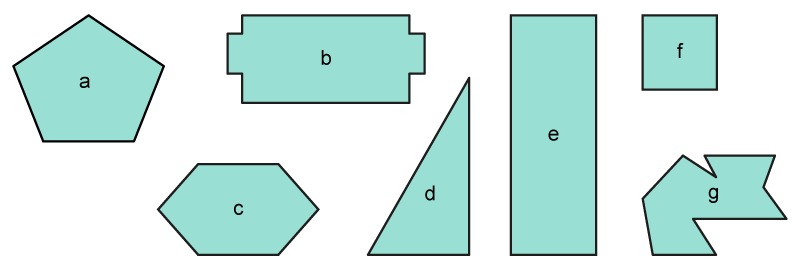
Example 1
Quadrilaterals
Let’s take a closer look at the quadrilaterals next. Some quadrilaterals have their own designations.

Definitions related to quadrilaterals
- A quadrilateral is a non-intersecting, closed polygonal chain of four segment lines
- A trapezium is a rectangle whose two sides are parallel.
- A parallelogram is a rectangle with two pairs of parallel sides.
- A rectangle is a parallelogram with one right angle
- A rhombus or diamond is a parallelogram with two adjacent sides of equal length.
- A square can be defined in two ways:
- 1) A rectangle with two adjacent sides of equal length.
- 2) A rhombus with one right angle.
Example 2
Let’s look at the following figures and their definitions.

- All of the patterns are quadrilaterals.
- Although only b looks like a trapezium, c, d, e and f also fulfill the criteria of a trapezium.
- The quadrilaterals c, d, e and f are parallelograms.
- Figures d and f are rectangles.
-
Figures e and f are rhombuses.
-
The definition of a square is only seen in figure f.