2. Basic concepts of geometry
Exercises
Basic concepts
Two-dimensional geometry studies plane patterns and their properties. The basic concepts of two-dimensional geometry are the point and the line.
The point has a place but no dimension. Thus, a point has no length, width, or height. It is expressed with a small circle or a cross. The point is then located at the centre of the circle or at the intersection of the cross. The names of points are usually capital letters. Because each point has its own place, there can be no two points with the same name in the same picture.
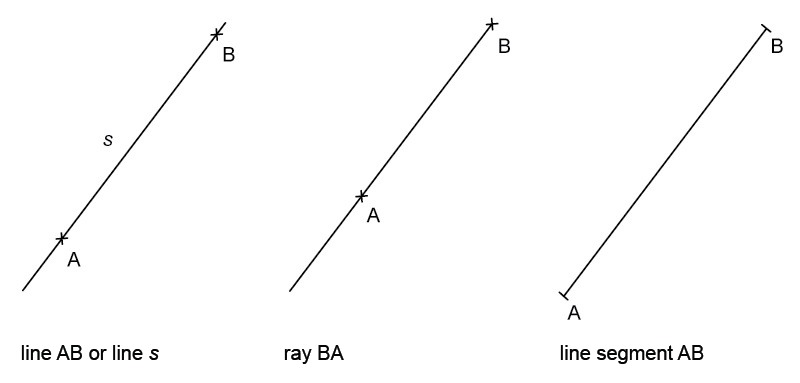
Only one line can be drawn through two points, named either by the points or by a lowercase letter. Although the line has a length, it cannot be measured because the line continues in both directions indefinitely.
Definitions of basic concepts of geometry
- A line starting from a point thought to be indefinitely extended in the other direction is called a ray.
- A line segment is the part of the line that exists between two points.
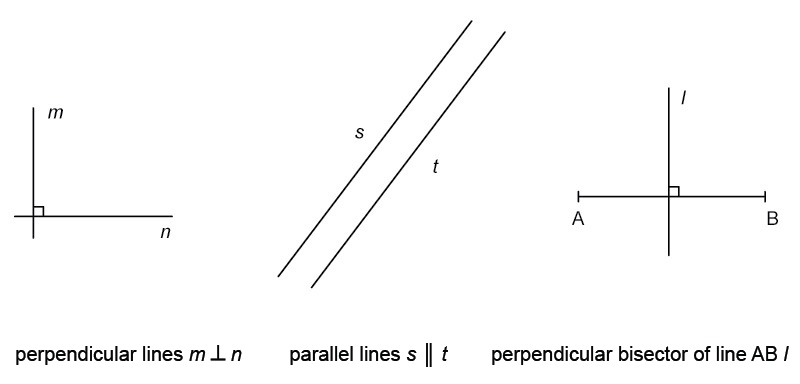
- If two lines are orthogonal to each other, they are called perpendiculars. Perpendicularity is denoted by the symbol [[$\bot$]].
- Parallel lines do not intersect. Parallelism is indicated by the symbol [[$\|$]].
- The perpendicular bisector of a line segment is a line that passes through the centre of the segment and is perpendicular to it.
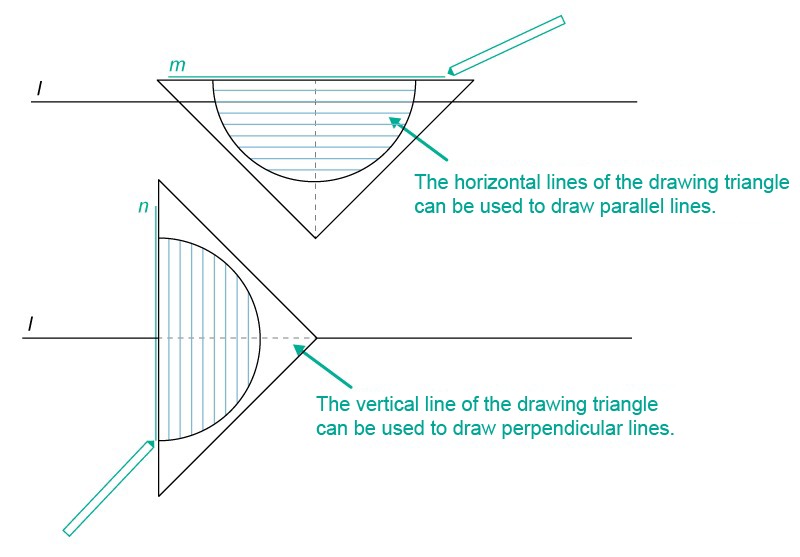
How to use a drawing triangle
Examples
Example 1
Determine the orthogonal distance of the point P from the line l .
Example 2
Draw the perpendicular bisector for the line segment AB.

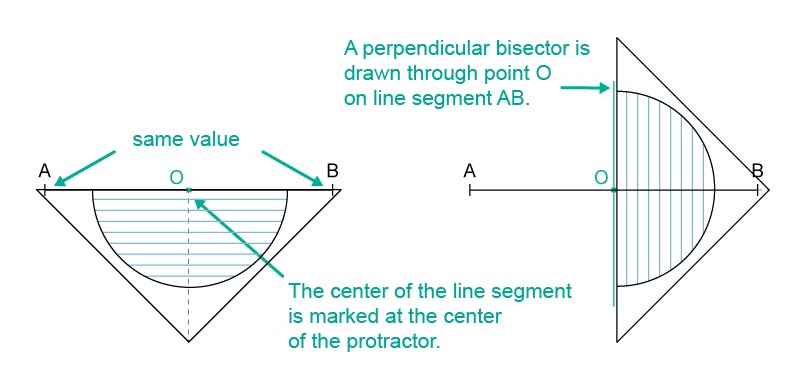
If a line segment is drawn in a coordinate system, the coordinates of the segment's midpoint can also be found by calculating the mean value of the [[$ <em>x $]] and [[$ <em>y $]] coordinates of the segment's endpoints.
Example 3
Calculate the coordinates of the midpoint of line segment AB when A [[$= (-3, 2)$]] and B [[$= (5, -6)$]].

You can check the answer by drawing.
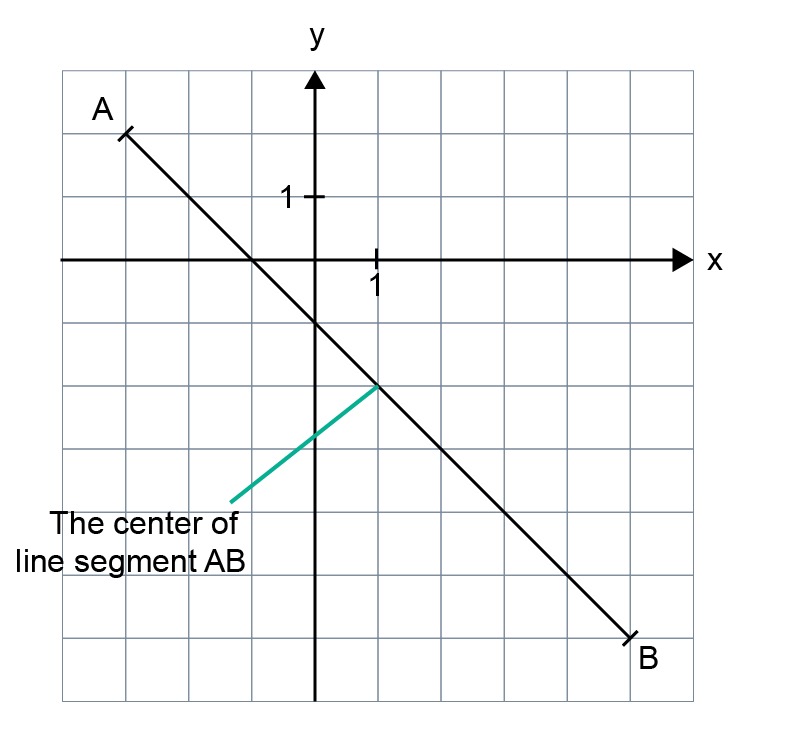
Answer: The midpoint of the line segment AB is [[$(1, -2)$]].