Like with fractions, the aim of rational expression calculations is to present the rational expression in the simplest possible form. A rational expression can be simplified if the numerator and denominator contain a common factor. A rational expression is in its simplest form when the only factor common to both the numerator and denominator is one.

Example 1

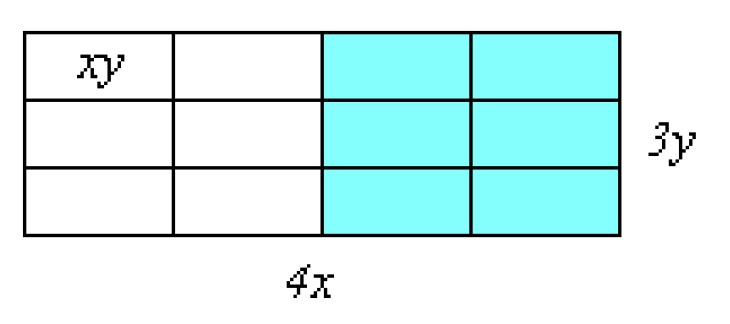
Simplify the rational expression [[$ \displaystyle\frac {4x \cdot 3y} {2} $]]​ by using the area model as an aid.

The area of a large rectangle is [[$ 4x \cdot 3y $]]​. On the other hand, the rectangle consists of [[$ 12 $]] small [[$ xy $]] rectangles, half of which are taken here. 

[[$ \displaystyle\frac {4x \cdot 3y} {2} = \displaystyle\frac {12xy} {2} = 6xy $]].

Example 2

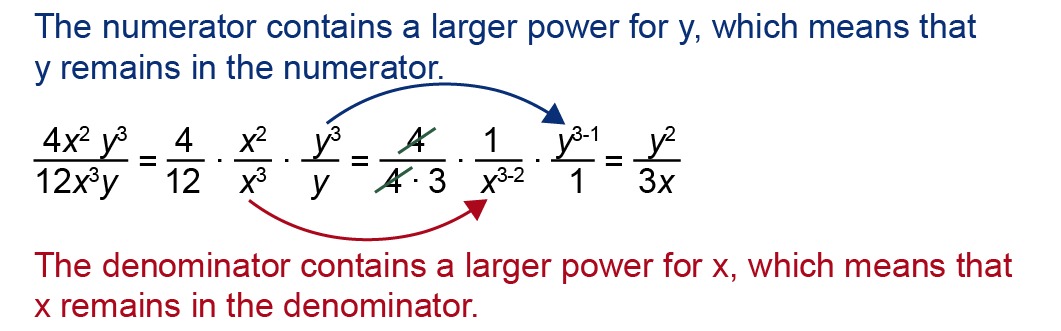
Simplify the rational expression [[$ \displaystyle\frac {4x^2y^3} {12x^3y} $]].​

Method I

The first monomial is divided by the second monomial so that the coefficients and similar variables are divided with each other. The value of similar powers comes on the side of the dashed line that initially has a higher power.

 

Method II

In general, a monomial is divided by a monomial by reducing the numerator and denominator by common factors without distinguishing between coefficients and variables.