Derivoinnin pikakurssi
-
Tunnin tärkein opetus: jos et osaa YO-kokeissa derivaattaa, älä tee derivaattatehtäviä. Todennäköisesti sana "derivaatta" esiintyy tällaisessa tehtävässä. Huomaa myös, että esimerkiksi [[$f'(4)$]] ei ole sama asia kuin [[$f(4)$]]. Pilkku [[$f$]]:n jälkeen tarkoittaa [[$f$]]:n derivaattaa.
Disclaimer: Tunnilla käsitellään vain oleellisimpia perusasiota. Pelkästään tämän tunnin pohjalta et tule osaamaan kaikkia derivaattatehtäviä.
Derivaatasta muualla
Matikkamatskut - kurssi 7
(perustuu Tekijän 7-kirjaan)
Opetus.tv: MAA6
Opetus.tv:llä ei ole omaa MAB7-kurssia.
Asian voi opetella myös vanhojen opetussuunnitelmien kirjoista, joita on saatavilla helposti kirjastoista ja puoli-ilmaiseksi käytettyinä. Esimerkiksi kirjaa Lyhyt Sigma 4 matemaattinen analyysi on tätä kirjoitettaessa saatavilla Helmet-kirjastoista tällä tavalla:
Disclaimer: Tunnilla käsitellään vain oleellisimpia perusasiota. Pelkästään tämän tunnin pohjalta et tule osaamaan kaikkia derivaattatehtäviä.
Derivaatasta muualla
Matikkamatskut - kurssi 7
(perustuu Tekijän 7-kirjaan)
Opetus.tv: MAA6
Opetus.tv:llä ei ole omaa MAB7-kurssia.
Asian voi opetella myös vanhojen opetussuunnitelmien kirjoista, joita on saatavilla helposti kirjastoista ja puoli-ilmaiseksi käytettyinä. Esimerkiksi kirjaa Lyhyt Sigma 4 matemaattinen analyysi on tätä kirjoitettaessa saatavilla Helmet-kirjastoista tällä tavalla:
| Kirjasto | Luokka | Tila | Ilmoitus |
|---|---|---|---|
| Herttoniemi aik | 510 | HYLLYSSÄ | -- |
| Kauklahti aik | 51.07 SIG | HYLLYSSÄ | -- |
| Laajasalo aik | 510 | HYLLYSSÄ | -- |
| Lauttasaari aik | 510 | HYLLYSSÄ | -- |
| Myyrmäki aik | 51.07 SIG | HYLLYSSÄ | -- |
| Paloheinä aik | 510 | HYLLYSSÄ | -- |
| Pasila aik | 510 | HYLLYSSÄ | -- |
| Pohjois-Haaga aik | 510 | HYLLYSSÄ | -- |
| Pointin kirjasto aik | 51.07 SIG | HYLLYSSÄ | -- |
| Töölö aik | 510 | HYLLYSSÄ | -- |
Hakusanoilla "derivaatta" tai "matemaattinen analyysi" löytyy Helmetistä paljon muitakin käyttökelpoisia kirjoja. Pitkän matematiikan kirjoissa asia esitellään vähän vaikeammin, mutta paljon selkeämmin.
TYKin iltaopetuksessa on pitkän matikan derivaattakurssi MAA6 tammikuussa alkavassa nelosjaksossa ja lyhyen matikan derivaattakurssi MAB7 huhtikuun puolessavälissä alkavassa kutosjaksossa.
Derivoi #1
Derivoi #2
Derivoi #3
Derivoi #4
Derivoi #5
Mitä derivaatta tarkoittaa ja mihin sitä käytetään
Derivaatta kertoo funktion kasvunopeuden. Esimerkiksi funktion [[$f(x)=2x^2 -3x$]] derivaatta on [[$f'(x)=4x-3$]], joten sen kasvunopeus
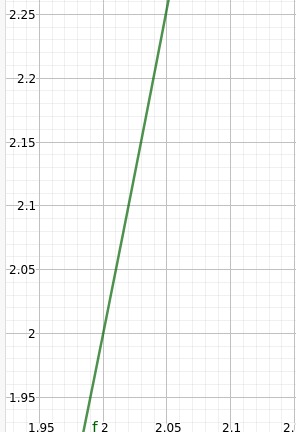
pisteessä 2 on [[$f'(2)=4\cdot 2-3 = 5$]]. Oikeanpuoleisessa kuvassa ollaan zoomattu funktioon kohdan [[$x=2$]] lähelle, ja funktio tosiaankin näyttää kasvavan tässä kohdassa n. 5 ruutua yhden vaakaruudun aikana.
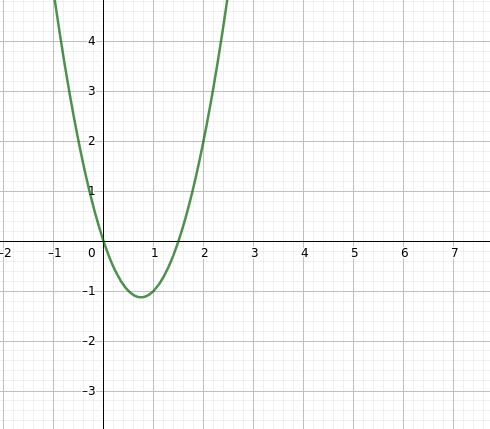
Lukiomatikassa ja YO-kirjoituksissa derivaatan suosituin käyttätarkoitus on funktion suurimpien ja pienimpien arvojen etsiminen. Nämä kohdat ovat yleensä funktion derivaatan nollakohdissa. Esimerkiksi ylläolevan funktion derivaatta oli [[$f'(x)=4x-3$]], josta voidaan laskea derivaatan nollakohta: jos [[$f'(x)=4x-3=0$]], on oltava [[$x=\frac{3}{4}$]]. Ylläolevasta kuvasta näkyy, että funktio saa tässä pienimmän arvonsa, joka on
[[$$f(\frac{3}{4})=2(\frac{3}{4})^2 -3\cdot\frac{3}{4} = -\frac{9}{8} .$$]]
Derivaatan nollakohdan lisäksi funktion suurin arvo voi olla sen määrittelyvälin päätepisteissä tai epäderivoituvuus/-jatkuvuuskohdissa. Tästä enemmän oppikirjoissa.
Esimerkki.
Kahvilan katuterassin aitaamiseen on käytettävissä 15 metriä köyttä. Terassista tehdään suorakulmio, ja yksi sitä rajaava sivu on ravintolan seinä. Mitkä terassin sivujen mitat on oltava, että sen pinta-ala olisi mahdollisimman suuri? Mikä pinta-ala tällöin on?
Ratkaisu.
Piiretään ensin kuva:
Vasemmalla mustalla on kahvilan seinä ja punaisella on terassia rajaava köysi. Jos merkataan kahta samanpituista sivua [[$x$]]:llä, kolmanteen sivuun jää köyttä [[$15-2x$]] metriä. Tällöin terassin pinta-ala on [[$A(x)=x\cdot (15-2x) = 15x-2x^2$]].
Derivoidaan pinta-alan funktio: [[$A'(x) = 15-4x$]]. Lasketaan derivaatan nollakohta: [[$15-4x=0$]], jos [[$4x =15$]], eli jos [[$x=3.75$]].
Tällöin kolmannen sivun pituus on [[$15-2\cdot 3.75=7.5$]] metriä, ja terassin mittojen pitäisi siis olla 3.75m x 7.5 m. Suurin mahdollinen pinta-ala terassille on siis [[$3.75\cdot7.5 = 28.125 \,\text{m}^2$]]
pisteessä 2 on [[$f'(2)=4\cdot 2-3 = 5$]]. Oikeanpuoleisessa kuvassa ollaan zoomattu funktioon kohdan [[$x=2$]] lähelle, ja funktio tosiaankin näyttää kasvavan tässä kohdassa n. 5 ruutua yhden vaakaruudun aikana.
Lukiomatikassa ja YO-kirjoituksissa derivaatan suosituin käyttätarkoitus on funktion suurimpien ja pienimpien arvojen etsiminen. Nämä kohdat ovat yleensä funktion derivaatan nollakohdissa. Esimerkiksi ylläolevan funktion derivaatta oli [[$f'(x)=4x-3$]], josta voidaan laskea derivaatan nollakohta: jos [[$f'(x)=4x-3=0$]], on oltava [[$x=\frac{3}{4}$]]. Ylläolevasta kuvasta näkyy, että funktio saa tässä pienimmän arvonsa, joka on
[[$$f(\frac{3}{4})=2(\frac{3}{4})^2 -3\cdot\frac{3}{4} = -\frac{9}{8} .$$]]
Derivaatan nollakohdan lisäksi funktion suurin arvo voi olla sen määrittelyvälin päätepisteissä tai epäderivoituvuus/-jatkuvuuskohdissa. Tästä enemmän oppikirjoissa.
Esimerkki.
Kahvilan katuterassin aitaamiseen on käytettävissä 15 metriä köyttä. Terassista tehdään suorakulmio, ja yksi sitä rajaava sivu on ravintolan seinä. Mitkä terassin sivujen mitat on oltava, että sen pinta-ala olisi mahdollisimman suuri? Mikä pinta-ala tällöin on?
Ratkaisu.
Piiretään ensin kuva:
Vasemmalla mustalla on kahvilan seinä ja punaisella on terassia rajaava köysi. Jos merkataan kahta samanpituista sivua [[$x$]]:llä, kolmanteen sivuun jää köyttä [[$15-2x$]] metriä. Tällöin terassin pinta-ala on [[$A(x)=x\cdot (15-2x) = 15x-2x^2$]].
Derivoidaan pinta-alan funktio: [[$A'(x) = 15-4x$]]. Lasketaan derivaatan nollakohta: [[$15-4x=0$]], jos [[$4x =15$]], eli jos [[$x=3.75$]].
Tällöin kolmannen sivun pituus on [[$15-2\cdot 3.75=7.5$]] metriä, ja terassin mittojen pitäisi siis olla 3.75m x 7.5 m. Suurin mahdollinen pinta-ala terassille on siis [[$3.75\cdot7.5 = 28.125 \,\text{m}^2$]]
YO-tehtäviä (suunnilleen helposta vaikeaan)
Huomaa, kuinika helposti derivaatta jää tässä tehtävssä huomaamatta:
