Let's draw two incomplete quadratic polynomial functions of the form [[$ f (x) = x^2 + bx $]] in the same coordinate system.

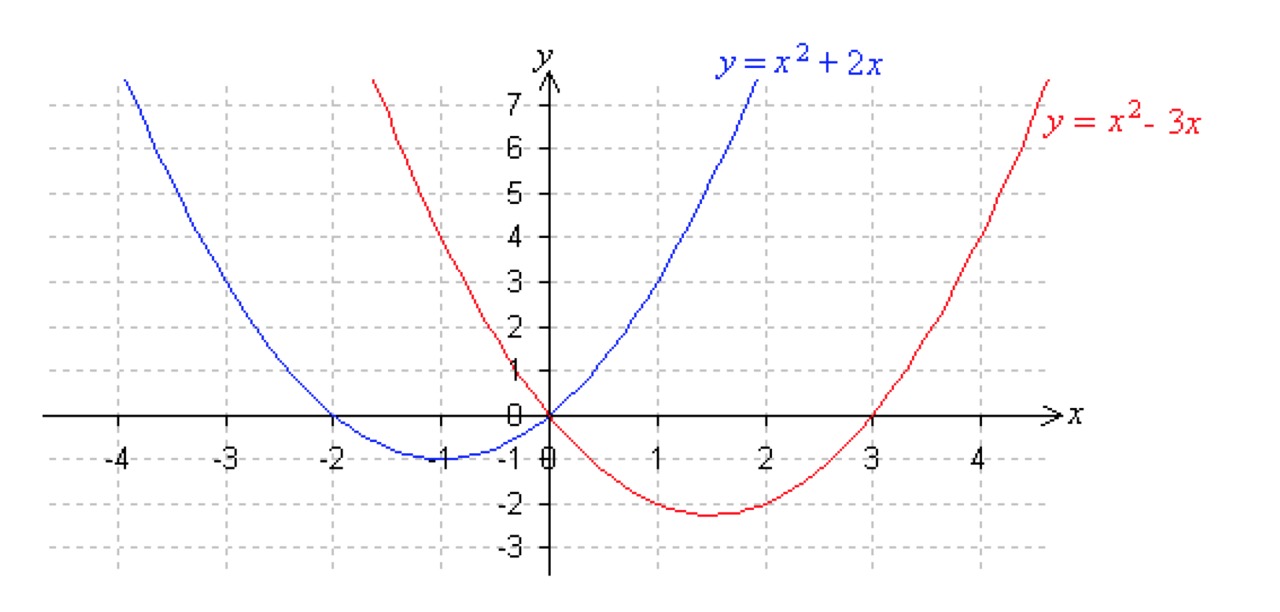
The graphs of the functions are congruent. The coefficient of the first-order term [[$ b $]] is clearly related to the second zero of the function and the position of the parabola's axis of symmetry.

Equations of the form [[$ y = ax^2 + bx $]] are most conveniently solved by dividing them into factors.

Example 1

Solve the equation [[$ 2x^2 + 6x = 0 $]] and sketch the graph of the parabola determined by the equation.

[[$ \begin{align*} 2x^2 + 6x &= 0 \;\;\; {\color {red} {\text {Divide the equation by factors.}}} \\ 2x(x + 3) &= 0 \\ \end{align*} $]]​

Apply the zero-product property.

[[$ \begin{align*} 2x &= 0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\text {or}}\;\;\;\;\;\; \;\;\;\;\;\; x + 3 &= 0 \\ x &= 0 \;\;\;\;\;\; \;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\; x &= -3 \\ \end{align*} $]]​

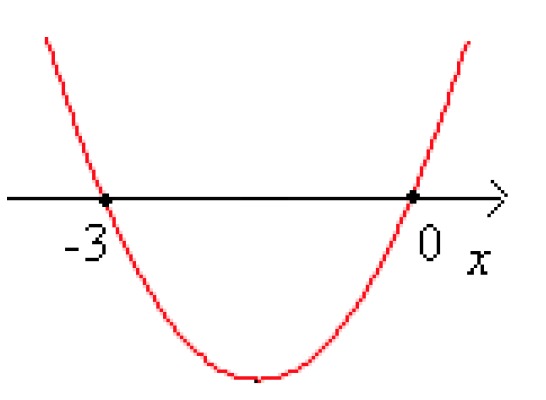
Answer: [[$ x = 0 $]]​ or [[$ x = -3 $]]​

Example 2

Solve the equation [[$ 5x^2 - 2x = 0 $]] and sketch the graph of the parabola determined by the equation.

[[$ \begin{align*} 5x^2 - 2x &= 0 \;\;\; {\color {red} {\text {Divide the equation by factors.}}} \\ x(5x - 2) &= 0 \\ \end{align*} $]]​

Apply the zero-product property.

[[$ \begin{align*} x &= 0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {\text {or}}\;\;\;\;\;\; \;\;\;\;\;\; 5x - 2 &= 0 \\ x &= 0 \;\;\;\;\;\; \;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\; 5x &= 2 \;\;\; {\color {blue} {||:5}} \\ x &&= \displaystyle\frac {2} {5} \end{align*} $]]​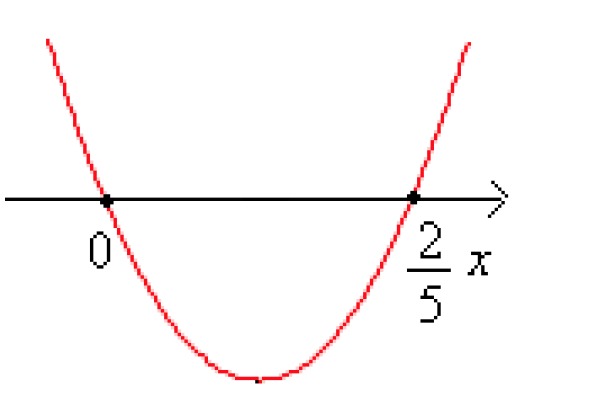

Answer: [[$ x = 0 $]]​ or [[$ x = \displaystyle\frac {2} {5} $]]​