There are usually two unknown variabless in a pair of equations. There are several computational solutions for a pair of equations. What is common to all of these solutions is that one of the unknown variabless is removed. The aim is to obtain only one equation with one variable. This equation is solved according to the usual rules of solving the equation. When the obtained solution is placed in one of the equations of the original pair of equations, one of the unknown variables is found.

Sometimes, the easiest way to eliminate the second variable of an equation is to add the equations together. The more you practice solving a pair of equations, the faster you will learn to find the most effective solution.

Example 1

Solve a pair of equations using the substitution method.

[[$ \begin{equation} \begin{cases}  x + y = 1 \\ x - y = 5 \\ \end{cases} \end{equation} $]]​

Solve the lower equation for [[$ y $]] and place the value of [[$ y $]] in the upper equation.

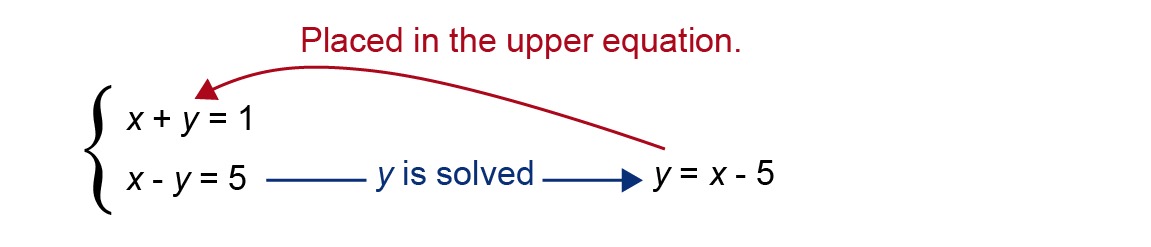
[[$ \begin{align*} x + {\color{red} {x - 5} } &= 1 \\ 2x &= 1 + 5 \\ x &= 3\end{align*} $]]

Place the resulting value [[$ x = 3 $]] in the equation [[$ y = x - 5 $]]. This gives you the result [[$ y = -2 $]].

Checking your answers:

Place the values in the equations and see if they hold:

[[$ 3 + (-2) = 1 $]]​ and [[$ 3 - (-2) = 5 $]]​

Both equations hold true, so the solutions are correct.

Answer: [[$ x = 3 $]]​ and [[$ y = -2 $]]​

Example 2

Solve the pair of equations by eliminating.

​[[$ \begin{equation} \begin{cases}  x + 2y = 1 \\ x - 2y = 5 \\ \end{cases} \end{equation} $]]​

Eliminate the variable [[$ y $]] from the equation. Both equations have the same number of the variable, but they are of opposite signs. By adding the equations together, the variables [[$ y $]] are canceled out.

[[$ \begin{equation} \begin{cases}  x + 2y = 1 \\ x - 2y = 5  \end{cases} \end{equation} \\ \\ \color {red}+ {\color {red} {\text {Both sides of the equations are added together.}}} $]]​

[[$ \begin{align*} x + 2y +x - 2y &= 1 +5 \ \\ 2x &= 6 \ \\ x &= 3 \end{align*} $]]​

Next, eliminate the variable [[$ x $]] from the equation. If the upper equation is multiplied by [[$ -1 $]] and the two equations are added together, the variable [[$ x $]] is canceled out.

[[$ \begin{equation} \begin{cases} x + 2y = 1 \; \; \; \; \; \; {\color {blue} {||·(-1)}} \ \\ x - 2y = 5 \\ \end{cases} \end{equation} \ \\ $]]​

[[$ \begin{equation} \begin{cases} -x - 2y = -1 \ \\ x - 2y = 5 \\ \end{cases} \end{equation} \ \\ \color {red}+ {\color {red} {\text {Both sides of the equations are added together.}}} $]]​

[[$ \begin{align} -x - 2y + x - 2y &= -1 + 5 \ \\ -4y &= 4 \ \\ y &= -1 \end{align} $]]​

Answer: [[$ x = 3 $]]​ and [[$ y = -1 $]]​

Example 3

Solve the following pair of equations.

​[[$ \begin{equation} \begin{cases} 5x - 2y = 10 \\ 2x + 4y = 4 \\ \end{cases} \end{equation} $]]​

If the upper equation is multiplied by two, the two variable [[$ y $]] can be canceled out.

[[$ \begin{equation} \begin{cases} 5x - 2y = 10 \; \; \; \; \; \; {\color {blue} {||·2}} \ \\ 2x + 4y = 4 \\ \end{cases} \end{equation} \ \\ $]]​

[[$ \begin{equation} \begin{cases} 10x - 2y = 20 \ \\ 2x + 4y = 4 \\ \end{cases} \end{equation} \ \\ \color {red}+ {\color {red} {\text {Both sides of the equations are added together.}}} $]]​

[[$ \begin{align} 10x - 4y + 2x + 4y &= 20+4 \ \\ 12x &= 24 \ \\ x &= 2 \end{align} $]]​

[[$ \begin{align*} 5 \cdot 2 - 2y &= 10 \\ -2y &= 10 - 10 \\ y &= 0\end{align*} $]]​

Answer: [[$ x = 2 $]]​ and [[$ y = 0 $]]​.

Note! Both the substitution and elimination methods were used to solve the pair of equations in Example 3.