Aihe 3: Epäoleellinen integraali ja jatkuva jakauma
Raja-arvo kun ylä- tai alaraja lähestyy nollaa?!
Epäoleellinen integraali [[$ \int_a^{\infty}f\left(x\right)dx $]] on raja-arvo [[$ \lim_{t\rightarrow\infty}\int_a^tf\left(x\right)dx $]], jos se on olemassa. Tälloin epäoleellinen integraali suppenee. Jos raja-arvo ei ole, epäoleellinen integraali hajaantuu. Integraali on epäoleellinen myös silloin jos ylä- tai alaraja on nimittäjän nollakohtaa.
f(x) on tiheysfunktio jos
1) f(x) >= kaikilla x:n arvoilla
2) f(x):n ja x-akselin rajoittama ala = 1.
Esimerkkinä normaalijakauman kertymäfunktio:
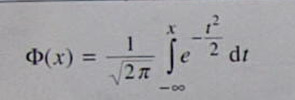
t. Pete
f(x) on tiheysfunktio jos
1) f(x) >= kaikilla x:n arvoilla
2) f(x):n ja x-akselin rajoittama ala = 1.
Esimerkkinä normaalijakauman kertymäfunktio:
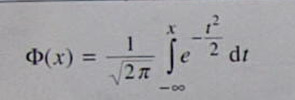
t. Pete