Tarkastellaan tässä vain pyörähdyskappaleen tilavuuden laskemista integroimalla. Ole tarkkana pyärähdysakselin suhteen!

Kun f(x) pyörähtää x-akselin ympäri, niin syntyneen pyörähdyskappaleen tilavuus V saadaan kaavalla

​[[$ V=\int_{a}^{b}\pi f(x)^{2}dx $]]​



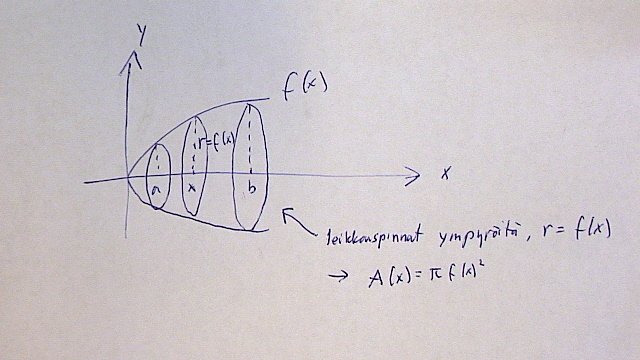
Jos f(x) = y pyörähtääkin y-akselin ympäri niin ratkaise ensin x = f(y) ja sitten integroit y:n suhteen normaalilla tavalla:

[[$ V=\int_{c}^{d}\pi f(y)^{2}dy $]].​


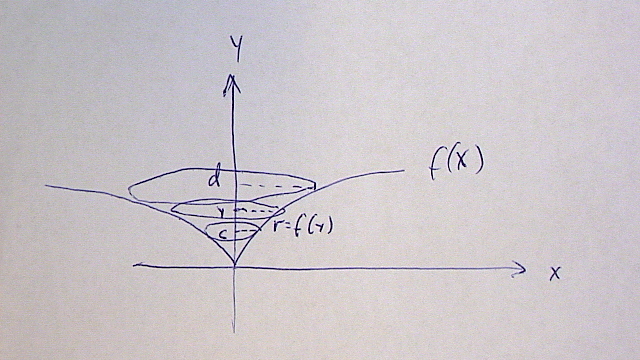
Muista tarkastaa että sinulla on käytössä oikeat integ.rajat c ja d!
_{t. Pete}