1. Lukujen suuruusjärjestyksen selvittäminen

Jos tehtävässä pitää laittaa lukuja suuruusjärjestykseen, luvuille voi tehdä joitain temppuja.

• Kun luvuissa on neliöjuuria ja mikään vertailtavista luvuista ei ole negatiivinen (nollaa pienempi), kannattaa kaikki korottaa toiseen potenssiin.
  Miinusmerkkisille luvuille pitää toiseen korotuksen jälkeen palauttaa miinusmerkki eteen, jotta suuruusjärjestys säilyy ennallaan. (Toiseen korotus "hävittää" luvun negatiivisuuden [[$ (-\sqrt{5})^2=5$]].)
  Kuutiojuurissa korotetaan kolmanteen jne. (Parittomilla potensseilla miinusmerkkikin säilyy, joten sitä ei tarvitse lisätä erikseen)
  Esimerkki:
  • Laita luvut [[$ 2\sqrt{3}$]], [[$4$]] ja [[$\sqrt{10}$]] suuruusjärjestykseen:
    toiseen korotus: [[$ (2\sqrt{3})^2$]], [[$4^2$]],[[$(\sqrt{10})^2$]]
    (Huom. ensimmäisessä luvussa pitää muistaa korottaa toiseen myös kerroin 2, koska tulon potenssi lasketaan korottamalla molemmat tekijät potenssiin: [[$(ab)^2=a^2 b^2$]])
    [[$4\cdot 3$]], [[$16$]], [[$10$]]
    [[$12$]], [[$16$]], [[$10$]]
    Alkuperäisistä luvuista suurin oli keskimmäinen ja pienin oli viimeinen luku. [[$ \sqrt{10}<2\sqrt{3}<4$]]
• Murtoluvut kannattaa laventaa tai supistaa samannimisiksi. Sen jälkeen osoittajista näkee suuruusjärjestyksen helposti.
• Desimaaliluvut voi muuttaa murtoluvuiksi, kun muistaa, että desimaaliosat ovat kymmenes-, sadas, -tuhannes-, jne. osia. (Esim. luku [[$0,123 = \frac{123}{1000}$]])
  • Voit muuttaa "helpot" murtoluvut desimaaliluvuiksikin, jos suuruusjärjestystä on helpompi tarkastella niin. (Esim. 1/2=0,5 ja 1/4=0,25 ja 3/5 = 0,2+0,2+0,2=0,6)

2. Eksponenttiyhtälön ratkaiseminen

• Yritä muuttaa kantaluvut samoiksi, jonka jälkeen tuntematon eksponentti ratkeaa merkitsemällä eksponenteissa esiintyvät lausekkeet yhtäsuuriksi.
  Esimerkki:
  
  • Ratkaise yhtälö [[$ 5^{3x+1}=125$]]
    ratkaisu
    [[$\begin{align} 5^{3x+1}&=125\space \| \text{luku 125 on sama kuin }5\cdot 5\cdot 5 \\5^{3x+1}&=5^3 \space \| \text{luvut ovat samat, kun eksponentit ovat yhtä suuret.} \\ 3x+1 &= 3 \\3x&=2 \\ x&=\frac{2}{3} \end{align}$]]

3. Potenssiyhtälön ratkaiseminen

• Muokataan ensin yhtälö muotoon "Tuntematon potenssiin joku luku on yhtä kuin joku luku."
• Otetaan puolittain potenssia vastaava juuri. Parillisilla potensseilla tulee plus- ja miinusratkaisu.
  Esimerkkejä:
  • Ratkaise yhtälö [[$5x^3=20$]]
    ratkaisu
    [[$ \begin{align}5x^3&=20 \space \| \text{ jaetaan vitosella.} \\ x^3&=4 \space \| \text{ otetaan 3. juuri}\\ x=\sqrt[3]{4}\end{align}$]]
    
    
  • Ratkaise yhtälö [[$7x^2=21$]]
    ratkaisu
    [[$ \begin{align}7x^2&=28 \space \| \text{ jaetaan seiskalla.} \\ x^2&=4 \space \| \text{ otetaan 2. juuri eli neliöjuuri. Parillinen potenssi: +,- !!!}\\ x&=\pm\sqrt{4} \\ x&=-2 \text{ tai } x=2\end{align}$]]

4. Epäyhtälön ratkaiseminen ("[[$=$]]"-merkin tilalla [[$>,\ge,<,\le$]] )

• Ensimmäisen asteen epäyhtälön voi ratkaista kuin se olisi yhtälö, mutta jos kerrotaan tai jaetaan miinusmerkkisellä luvulla puolittain, suuruusjärjestyksen suunta pitää vaihtaa.
  Esimerkki:
  • Ratkaise epäyhtälö [[$-15x+3>3x-2$]]
    • ratkaisu
      [[$\begin{align} -15x+3&>3x-2\\-15x-3x&>-2-3 \\-18x&>-5 \space \| \text{ jaetaan luvulla -18. Merkin suunta vaihtuu.}\\x&<\frac{5}{18} \end{align}$]]
• Toisen asteen epäyhtälöissä siirretään kaikki termit vasemmalle ja tutkitaan merkin vaihtumiskohtaa, eli etsitään ensin nollakohdat. Etumerkkiä nollakohtien eri puolilla tarkastellaan tyyppikuvaajan avulla (2. asteen lausekkeella paraabeli, ylös tai alas aukeava).
  Esimerkki
  Ratkaise epäyhtälö [[$-3x^2-2>4x-1$]]
  • Muokataan epäyhtälöä muotoon, jossa oikealla puolella on pelkkä nolla: [[$\begin{align}-3x^2-2& >4x-1\\-3x^2-2-4x+1&>0\\-3x^2-4x-1&>0\end{align}$]]
    
    
  • Etsitään nollakohdat ratkaisemalla yhtälö [[$-3x^2-4x-1=0$]] ratkaisukaavan avulla:
    [[$x=\frac{-(-4)\pm \sqrt{(-4)^2-4\cdot (-3)\cdot (-1)}}{2\cdot (-3)}=\frac{4\pm\sqrt{16-12}}{-6}=\frac{4\pm2}{-6}$]]
    [[$x= \frac{4-2}{-6}=-\frac{1}{3}$]] tai [[$x=\frac{4+2}{-6}=-1 $]]
    
    
  • Luonnostellaan lausekkeen [[$-3x^2-4x-1$]] tyyppikuvaaja edellä saatujen nollakohtien avulla:
    
    
    Alaspäin aukeava paraabeli, koska [[$x^2$]]-kerroin on negatiivinen
    
    
  • Luetaan epäyhtälölle ratkaisu kuvaajasta. (Pitikö olla suurempaa vai pienempää kuin nolla...)
    Kuvaajasta nähdään, että [[$-3x^2-4x-1>0,$]] kun [[$-1<x<-\frac{1}{3}$]]
    
    
  • Näin saadaan alkuperäisen tehtävän ratkaisuksi [[$-1<x<-\frac{1}{3}$]].

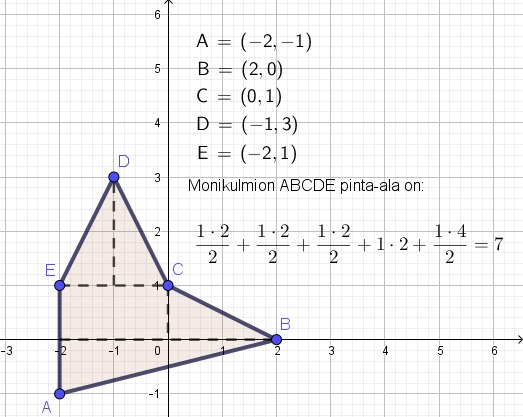
5. Pinta-alan laskeminen koordinaatistoruudukossa

• Paloittele monikulmio suorakulmaisiin kolmioihin, joiden pinta-alat lasket yhteen.
  Suorakulmaisen kolmion kanta ja korkeus ruutuina vaaka- ja pystysuoraan.
  • Kolmion pinta-ala on kanta kertaa korkeus jaettuna kahdella.
• Voit käyttää myös valmiita kaavoja:
  • Suorakulmion ala = kanta kertaa korkeus
  • Suunnikkaan ala on yhdensuuntaisten sivujen pituus kertaa niiden välinen etäisyys.
  • Puolisuunnikkaan ala on yhdensuuntaisten sivujen keskiarvo kertaa niiden välinen etäisyys.
  • Ympyrän ala on pii kertaa säde toiseen potenssiin [[$A=\pi r^2$]].