Aihe 2: Suorakulmaisen kolmion sin, cos, tan
Suorakulmaisen kolmion sin, cos, tan
Tuttu aihe jo yläkoulusta, eli suorakulmaisen kolmion sini, kosini ja tangentti (allaoleva kuva MAOLin taulukkokirjan s. 36).

Sin, cos ja tan liittyvät kolmioiden yhdenmuotoisuuteen, mutta siitä viis kunhan osaatte ratkaista niiden avulla sivujen pituuksia tai kulmia. Pointti on se, että jokaisessa trig. funktiossa on kolme suuretta: esim. sinin kaavassa
sin a = vast/hyp
suureet ovat a = kulma, vast = kulman a vastainen kateetti ja hyp = suorakulmaisen kolmion pisin sivu eli hypotenuusa. Jos noista tiedetään mitkä kaksi tahansa, niin kolmas voidaan ratkaista.
Sivut vast tai hyp ratkaistaan laskemalla laskimella sin a:n likiarvo ja kertomalla saatu yhtälö ristiin. Kulma a taas ratkaistaan laskemalla ensin jakolasku vast/hyp ja ottamalla saadusta desimaaliluvusta laskimella KÄÄNTEINEN SIN = SIN-1
Kosini ja tangentti on määritelty seuraavasti:
cos a = vier/hyp
tana = vast/vier

Sin, cos ja tan liittyvät kolmioiden yhdenmuotoisuuteen, mutta siitä viis kunhan osaatte ratkaista niiden avulla sivujen pituuksia tai kulmia. Pointti on se, että jokaisessa trig. funktiossa on kolme suuretta: esim. sinin kaavassa
sin a = vast/hyp
suureet ovat a = kulma, vast = kulman a vastainen kateetti ja hyp = suorakulmaisen kolmion pisin sivu eli hypotenuusa. Jos noista tiedetään mitkä kaksi tahansa, niin kolmas voidaan ratkaista.
Sivut vast tai hyp ratkaistaan laskemalla laskimella sin a:n likiarvo ja kertomalla saatu yhtälö ristiin. Kulma a taas ratkaistaan laskemalla ensin jakolasku vast/hyp ja ottamalla saadusta desimaaliluvusta laskimella KÄÄNTEINEN SIN = SIN-1
Kosini ja tangentti on määritelty seuraavasti:
cos a = vier/hyp
tana = vast/vier
- Taas opetus.tv:stä, katso ainakin videot 2-4: Trigonometriset funktiot
- Itse tehty video taulukkokirjan kaavoista: http://www.youtube.com/watch?v=V5Oo7PENOPY
- Video sivun pituuden ratkaisemisesta kosinin avulla, sinin ja tangentin avulla toimittas ihan samalla tavalla: http://youtu.be/HQFlRx7m0lE
- Vielä yksi oma esimerkki kulman ratkaisemisesta tangentilla: http://youtu.be/sVox5lilsjw
- Sama englanniksi: Khan Academyn Basic Trigonometry part 1
- Jatkuu: Khan Academyn Basic Trigonometry part 1
- Monimutkaisempi Khan Academyn Trigonometry Problem, mutta ymmärrätte luultavasti tosi hyvin mistä on kysymys vaikka englanninkieli voi tuottaa vaikeuksia (matematiikan merkit on kaikkialla samoja!). Ratkaisussa hienostellaan ja käytetään tarkkoja arvoja + Pythagorasta mutta se menis kokonaisuudessaan sincostanillakin ja likiarvoillakin(tee se itse, saat plussaa..!?): Trig. Problem
- Edellisen sanallisen tehtävän loppuosa: Part 2
Liitteet:
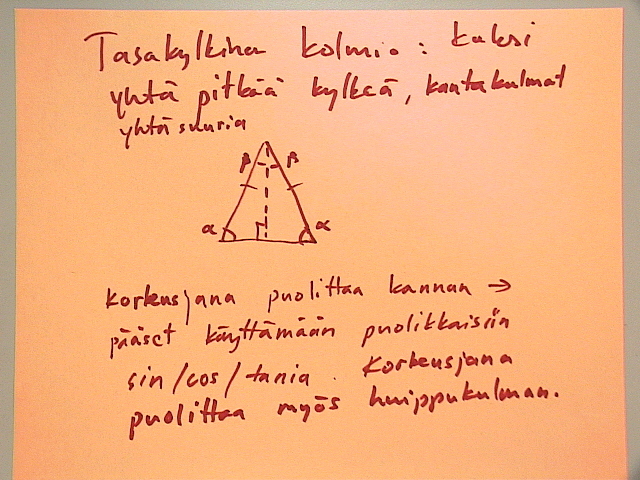
Tasakylkinen ja tasasivuinen kolmio
Nämä eivät ole suorakulmaisia joten et voi käyttää sin/cos/tania. MUTTA: kannalle piirretty korkeusjana puolittaa sekä kannan että huippukulman. Saat siis kaksi identtistä SUORAKULMAISTA kolmiota, joihin voit käyttää trigonometriaa ja Pythagorasta.
Alla vielä laskuesimerkki, jossa tiedetään tasakylkisen kolmion kylki ja huippukulma ja kysytään alaa (kolmion alanhan kaikki osaa laskea..?):
