2.1 Kuvaajan piirto ja analyysi
Kuvaajan piirtäminen
Fysiikassa keskeinen menetelmä on mittaustulosten mallintaminen kuvaajina ja kuvaajien analysointi. Kuvaajissa mittapisteet sijoitetaan koordinaatistoon, jolloin pistejoukon muoto paljastaa mitattujen suureiden välisen riippuvuuden. Riippuvuuden selvittämiseksi kuvaajaa analysoidaan. Mittaustulokset ovat usein erillisinä liitetiedostona, mutta mittaustulokset voidaan antaa myös tehtäväannon yhteydessä.
Kuvaajien tuottamiseen on koejärjestelmässä useita ohjelmistoja, mutta näissä harjoituksissa käytetään Logger Pro:ta. Logger Pro on erittäin käytännöllinen ohjelmisto fysiikan ylioppilaskokeen vaatimuksiin.
Kuvaajan piirtäminen (Logger Pro -ohjelmalla)
YTL:n tiedotteiden mukaan "Mittausaineistoa voidaan antaa osana tehtävänantoa tai erillisinä tiedostoina, jotka tarjotaan useissa eri formaateissa". Pidetyissä ylioppilaskokeissa data on annettu lähes kaikissa mahdollisissa formaateissa, kuten csv-taulukkomuodossa, laskin ohjelmien tiedostoina, GeoGebra-tiedostona ja Logger Pro -tiedostona. Annetuissa tiedostoissa on data taulukoituna, joten kuvaajan tuottaminen tehdään itse.
Mittauspisteistä kuvaajaan
Mittauspisteiden cmbl-liitetiedosto avataan Logger Pro -ohjelmalla. Data on annettu taulukkona sarakkeissa. Kuvaaja piirretään valikon Lisää alavalikosta Kuvaaja. Tarkista että akselit ovat haluamassasi järjestyksesssä ja että yksiköt ja suureet on merkitty oikein.
Kuvaajan oikeanlainen esitys
Kun kuvaaja on lisätty, oletuksena saattaa olla murtoviivaesitys, jossa mittauspisteet yhdistyvät janoilla toisiinsa. Murtoviivaesitys ei kelpaa kuin erikoistapauksissa, joissa mittauspisteitä on hyvin tiheässä eikä sopivaa sovitekäyrää löydy. Kuvaajan asetuksista valitaan mittauspisteet näkyviin ja poistetaan valinta Yhdistä pisteet. Mittauspisteitä mallinnetaan sopivalla sovitekäyträllä, esimerkiksi alla olevan kuvan lineaarisella sovituksella.
Jos mittauspisteitä on paljon (kymmeniä) ja niihin ei löydy järkevää sovitetta, voidaan pisteet yhdistää murtoviivalla. Tällöin kuvaajalle ei saada yhtälöä, mutta sen osia voidaan analysoida muutoin. Alla olevassa kuvaajassa oikeanpuoleisessa kuvaajassa on Yhdistä pisteet -toiminto valittuna. Vasemmanpuoleisessa kuvaajassa mittauspisteet ovat toistensa päällä, mikä tekee kuvaajasta epäsiistimmän näköisen.
Muodostuneesta kuvaajasta tarkistetaan, että pysty- ja vaaka-akselit ovat oikein päin. Akselin suureen valintaa voidaan muuttaa akselin nimen kohdalta. Akseleiden valinta tehdään tehtävään liittyvien lakien perusteella ellei sitä suoraan kerrota tehtävässä. Jos vaaka-akselille vaaditaan suure [[$a$]] ja pystyakselille [[$b$]], voidaan se ilmaista useilla tavoilla.
- "Esitä suureen [[$b$]] riippuvuus [[$a$]]:sta"
- "Piirrä [[$(a,b)$]]-kuvaaja"
- "Piirrä kuvaaja, jossa suure [[$b$]] on suureen [[$a$]] funktiona"
- "Piirrä [[$b(a)$]]"
Akseleit nimetään suureen nimellä tai tunnuksella sekä suureen yksiköllä. Sopivat akselien nimet ovat esimerkiksi [[$\mathrm{Nopeus (m/s)}$]] tai [[$v(\mathrm{m/s})$]]. Kuvaajaa analysoidaan tehtäväannon mukaisella tavalla ennen kuin se liitetään vastauskenttään.
Kuvaajan liittäminen vastauskeen
Kuvaaja liitetään kuvakaappauksena. Tarvittaessa liitetään otetaan useita kuvakaappauksia, jotta on selvää, mitä analyysitoimenpiteitä on tehty. Kuvakaappauksen voi tallentaa kuvana ja avata piirto-ohjelmassa, jos siihen on tarve tehdä lisämerkintöjä.
Vastauskenttään liitetyn kuvakaappauksen yhteyteen perustellaan kuvaajalla tehtävät / tehdyt analyysitoimenpiteet. Vastaukseen liitetystä kuvaajasta on käytävä ilmi analyysitoimenpide, joka on tehty.
- Jos kuvaajalta luetaan arvoja (interpolointi/ekstrapolointi), otetaan kuvankaappaus kohdasta, jossa luettu kohta näkyy.
- Suoran / käyrän sovitus ja sen parametrit (esimerkiksi kulmakerroin) näkyvät kuvankaappauksessa.
- Graafinen integrointi tai derivointi tuloksineen (lukuarvo ja yksikkö) ovat kuvaajassa näkyvissä.
Pisteiden mallintaminen sovitekäyrällä
Tieto luonnonilmiöistä syntyy mittausten perusteella. Mitattaessa kahta suuretta on mielekästä tarkastella suureiden riippuvutta toisistaan kuvaajan avulla. Suureet sijoitetaan vaaka- ja pystyakseleille. Mittauspisteiden muodostamasta joukosta nähdään, sijoittuvatko pisteet suoralle tai muodostavavatko ne jonkin muun säännönmukaisen käyrän.
Suoran tai käyrän sovittaminen on tulosten mallintamista. Tällöin idealisoidaan tulokset yksinkertaisen matemaattisen funktion mukaiseksi. YO-tehtävissä tilanne on tavallisesti sellainen, että tehtävässä selvitetään mitattujen suureiden välinen riippuvuus tai aiheen teorian perusteella tiedetään, millaista mallia tulosten pitäisi noudattaa. Suoran tai käyrän sovituksella korjataan yksittäisiin mittauspisteisiin sisältyviä satunnaisia mittausvirheitä ja saadaan suureiden riippuvuutta parhaiten mallintava matemaattinen yhtälö.
Lineaarinen riippuvuus ja suoran yhtälö
Kun mittauspisteet asettuvat (likimäärin) suoralle, voidaan suureiden välillä todeta lineaarinen riippuvuus. Tällöin niiden välinen yhtälö on suoran yhtälö. Suoran yhtälö on yleisesti muotoa [[$ y=kx+b $]], jossa [[$y$]] ja [[$x$]] ovat muuttujat, [[$k$]] on suoran kulmakerroin sekä [[$b$]] suoran ja pystyakselin leikkauskohta. Fysiikassa [[$x$]] ja [[$y$]] vastaavat mitattuja suureita ja kulmakerroin on suure, joka yhdistää mitatut suureet toisiinsa. Vakiotermi on samaa suuretta kuin pystyakselin suure [[$y$]]. Kulmakerroin on usein tehtävissä olennaisin parametri, mutta vakiotermillä voi olla oma merkityksensä erityisesti, jos se poikkeaa selvästi nollasta pystyakselin mittauspisteiden arvoihin verrattuna.
Kulmakerroin on suureiden osamääränä siten, että [[$ k=\frac{\Delta y}{\Delta x} $]]. Ilmaisu tarkoittaa, että suureiden muutosten suhde on vakio eli kulmakerroin on sama laskettuna mistä tahansa kohdasta suoraa. Lineaarinen sovitus voidaan tehdä mittausohjelmistolla. Ohjelmisto kertoo suoran yhtälön, joten suoran parametrit [[$k$]] ja [[$b$]] saadaan automaattisesti.
Epälineaarinen riippuvuus ja käyrän sovitus
Mikäli mittauspisteet eivät muodosta suoraa, mallinnetaan tilannetta käyrällä. Kaksi erityyppistä tilannetta voi tulla vastaan.
Tilanne 1 - Ei tietoa sopivasta matemaattisesta mallista
Jos suureiden väliselle riippuvuudelle ei ole selkeää matemaattista mallia, valitaan Logger Pro:n Käyrän sovitus -valikosta silmämääräisesti parhaiten pisteisiin sopiva käyrä. Tämän jälkeen käyrää voidaan analysoida. Käyrän muodolla mittauspisteiden rajoittaman alueen ulkopuolella ei ole merkitystä, eikä ekstrapolointi ennen ensimmäistä tai viimeisen mittauspisteen jälkeen ole kovin mielekästä. Yleisesti ottaen tarpeeksi korkean asteen polynomifunktio saadaan sovitettua mihin muotoon tahansa, joten Logger Pro:n 5. asteen polynomi (korkein mahdollinen) on varsin käytännöllinen.
Tilanne 2 - Suureiden välinen teoreettinen riippuvuus on tiedossa
Jos suureiden välinen epälineaarinen riippuvuus on teoreettisesti tunnettu, sovitetaan pistejoukkoon juuri oikea käyrä. Tällöin sovituksen parametreja voidaan hyödyntää tehtävässä. Esimerkiksi radioaktiivisen näytteen aktiivisuuden riippuvuus ajan suhteelle on yleisesti tiedossa oleva matemaattinen malli. Tiedetään, että aktiivisuus vähenee eksponentiaalisesti hajoamislain mukaan [[$ A=A_0 e^{-\lambda t} $]].
Sijoitetaan pisteet mittausohjelmaan, sovitetaan eksponentiaalinen käyrä, josta saadaan parametrina hajoamisvakio [[$ \lambda $]], jonka perusteellla voidaan laskea esimerkiksi puoliintumisaika.
Kuvaajan analyysimenetelmät
Kulmakerroin ja muutosnopeus
Suoran sovituksessa saatavan yhtälön keskeinen parametri on suoran kulmakerroin. Kulmakerroin kuvaa lineaarisen funktion muutosnopeutta. Kulmakerroin voidaan määrittää minkä tahansa kahden pisteen välillä, jolloin saadaan keskimääräinen muutosnopeus. Esimerkiksi [[$(t,x)$]]-koordinaatistossa kuvaajalta valittujen pisteiden välinen kulmakerroin on keskinopeus.
Huomaa, että keskinopeus voidaan laskea taulukoitujen arvojen perusteella ilman kuvaajaa. Kahden pisteen välinen keskinopeus ei myöskään ole täsmälleen sama asia kuin koko pistejoukkoon sovitetun suoran kulmakerroin.
Kulmakerroin matemaattisesti
Kuvaajalta valitun kahden pisteen välinen kulmakerroin [[$k$]] on pisteiden [[$y$]]-koordinaattien muutoksen [[$\Delta y$]] ja [[$x$]]-koordinaattien muutoksen [[$\Delta x$]] osamäärä.
[[$k=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}$]]
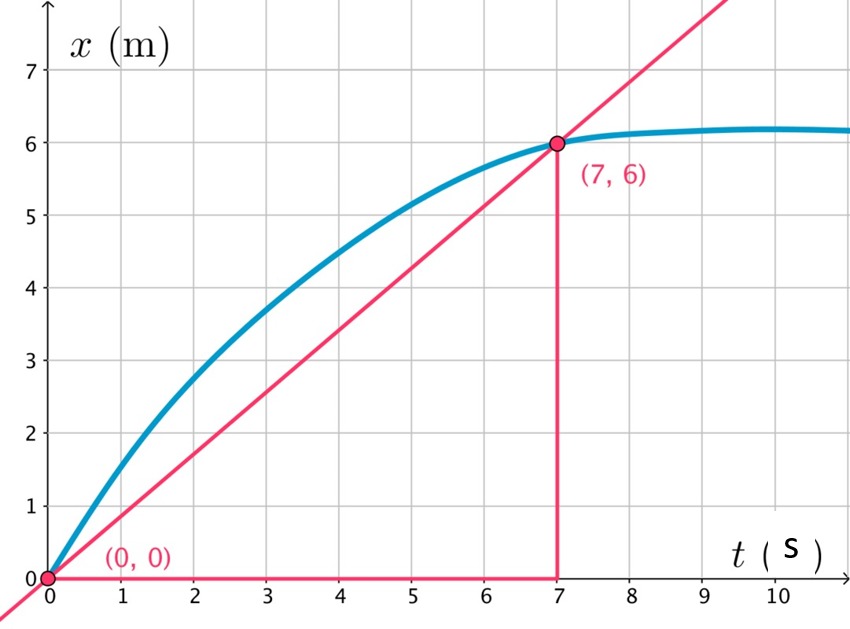
Kappaleen keskinopeus välillä 0,0...7,0 s on
[[$ v_k=\dfrac{\Delta x}{\Delta t} =\dfrac{\text{6,0 m}-\text{0,0 m}}{\text{7,0 s}-\text{0,0 s}} \approx \text{0,86 m/s} $]]
Keskimääräinen muutosnopeus ilmaistaan [[$\Delta$]]-merkkiä käyttäen. Keskinopeus [[$v_k=\dfrac{\Delta x}{\Delta t}$]] tai keskikiihtyvyys [[$a_k=\dfrac{\Delta v}{\Delta t}$]].
Mitä tahansa ajan suhteen laskettua muutosta voidaan kutsua muutosnopeudeksi. Paikan muutos ajan suhteen on nopeus. Nopeuden muutosnopeus ajan suhteen on kiihtyvyys. Radioaktiivisen näytteen ytimien hajoamisten määrän muutosnopeus ajan suhteen on aktiivisuus.
Graafinen derivointi
Jos määritetään käyrän kulmakerrointa pienemmällä ja pienemmällä välillä, päädytään käyrän derivaattaan. Käyrälle piirretty tangentti on suora, joka leikkaa käyrää vain yhdessä pisteessä eli sivuaa käyrää. Käyrälle piirretyn tangentin kulmakerroin on kuvaajan derivaatta eli se kuvaa käyrän hetkellistä muutosnopeutta. Videolla tutkitaan paikan kuvaajan avulla kappaleen nopeutta. [[$(t,x)$]]-koordinaatistossa kuvaajalle piirretty tangentti kuvaa kappaleen hetkellistä nopeutta. Käyrälle sijoitetun tangentin kulmakerroin (eng. slope) suurenee mittauksen edetessä, eli kappaleen nopeus kasvaa (käyrä jyrkkenee), kunnes kappale pysähtyy (kuvaaja muuttuu vaakasuoraksi). Kulmakertoimen suuruus on liikkeen hetkellinen nopeus.
https://peda.net/id/889ec002a0f
Tangentin kulmakertoimen määrittämistä kutsutaan graafiseksi derivoinniksi. Hetkellinen nopeus ilmoitetaan matemaattisesti [[$v=\dfrac{dx}{dt}$]] (derivoidaan paikan kuvaajaa ajan suhteen).
Graafinen integrointi
Fysiikassa monet suureet määritellään kahden suureen välisenä tulona. Esimerkiksi matka tasaisessa liikkeessä on nopeuden ja ajan tulo, [[$ s=vt $]]. Tai siirtymän ja ajan muutoksen merkinnöillä: [[$ \Delta x=v\Delta t $]]. Muuttuvassa liikkeessä matka voidaan määrittää vastaavalla periaatteella. Nopeuden kuvaaja jaetaan hyvin aikaväleihin [[$ \Delta t_1 $]], [[$ \Delta t_2 $]]..., joissa nopeus on vakio. Tällöin voidaan laskea kappaleen kulkema matka osissa.
[[$ \quad s_1+s_2+s_3... = v_1 \Delta t_1 +v_2 \Delta t_2 +v_3 \Delta t_3+... $]]
Graafisesti "paloittain laskeminen" tarkoittaa pinta-alan määrittämistä. Matemaattinen nimitys menetelmälle on graafinen integrointi. Matkan määrittäminen graafisesti integroimalla merkitään [[$\int vdt$]]. Menetelmää ilmentää alla oleva kuva. Oikeanpuoleisessa kuvassa aikaväli on äärimmäisen lyhyt, jolloin käyrän ja vaaka-akselin väliin jäävä ala tarkasti määritettyä.

Mittausohjelmistossa on toiminto graafisen integroinnin suorittamiselle. Graafisesta esityksestä rajataan sopiva väli ja ohjelmisto määrittää intgraalin arvon ja yksikön.
Graafinen integrointi
Kuvaajan ja vaaka-akselin välisen pinta-alan likimääräistä määrittämistä kutsutaan graafiseksi integroinniksi. Fysiikassa pinta-ala ilmentää suuretta, joka on akselien suureiden välinen tulo. Integraali voidaan määrittää mittausohjelmistolla tai jakamalla alue sellaisiin monikulmioihin, joiden ala on helppo laskea.
Esimerkkejä graafisesta integroinnista
Nopeuden muutos
[[$(t,a)$]]-koordinaatistossa fysikaalinen pinta-ala kuvaa nopeuden muutosta, [[$ \Delta v=\int adt$]].
Sähkövaraus
[[$(t,I)$]]-koordinaatistossa fysikaalinen pinta-ala kuvaa siirtynyttä sähkövarausta, [[$ Q=\int Idt $]].
Voiman tekemä työ
[[$(s,F)$]]-koordinaatistossa fysikaalinen pinta-ala kuvaa voiman tekemää työtä, [[$ W=\int Fds $]].
Voiman impulssi
[[$(t,F)$]]-koordinaatistossa fysikaalinen pinta-ala kuvaa voiman aiheuttamaa impulssia, [[$I=\int Fdt$]].
Arvojen lukeminen kuvaajasta
Pistejoukkoon sovitetulta käyrältä voidaan lukea arvoja, jotka eivät ole mittauspisteitä. Jos luettu arvo on mittauspisteiden välistä, on kyseessä interpolointi. Jos pisteet ovat ennen ensimmäistä mittauspistettä tai viimeisen jälkeen, on kyseessä ekstrapolointi. Ekstrapolointia tehdessä on oltava tiedossa, että käyrän mukainen malli on voimassa. Kuvaajanpiirto-ohjelmissa on mahdollista lukea annettuja arvoja tai sijoittamalla tarvittavat arvot käyrän yhtälöön.
Lasketun sarakkeen tekeminen ja käyttö
Soveltammissa tehtävissä mittausdata aineistoa on käsiteltävä ennen kuin kuvaaja piirretään. Mitattujen suureiden avulla lasketaan uusi suure, joka sijoitetaan kuvaajan akselille. Taulukkoon tehdään uusi laskettu sarake, johon uuden suureen arvot tulostuvat. Pisteitä ei tarvitse laskea yksitellen, vaan ohjelmaan annetaan matemaattinen kaava, joka laskee automaattisesti uudet arvot.
Kuvaajatehtävien aineistossa oleva mittausdata on lähtöarvo, joten siihen ei tarvitse erikseen viitata tehtävää ratkaistaessa. Jos kuitenkin lasketaan uusi sarake, on vastauksessa mainittava uuden lasketun sarakkeen tekeminen ja miten arvot uuteen laskettuun sarakkeeseen saadaan.
Idealisoidun kuvaajan piirtäminen
Tehtävissä voidaan pyytää piirtämään kuvaaja, vaikka erillisiä mittauspisteitä ei anneta. Esimerkiksi kappale liikkuu ensimmäiset 5 sekuntia tasaisesti kiihdyttäen ja seuraavat 5 sekuntia tasaisesti saavuttamallaan loppunopeudella. Piirretään nopeuden kuvaaja. Tällaisissa tehtävässä kuvaajan piirtämiseksi tarvittavat mittauspisteet lasketaan itse. Mittauspisteitä ei tarvitse laskea jokaisen sekunnin kohdalla, vaan riittävät pisteet saadaan, kun on tiedossa piste liikkeen alussa ja loppussa tai liikkeen muuttuessa. Esimerkin tapauksessa on selvitettävä piste hetkellä 0 sekuntia, hetkellä 5 sekuntia (tasaisesti kiihtyvä liike päättyy ja tasainen liike alkaa) ja hetkellä 10 sekuntia. Saadut arvot sijoitetaan kuvaajanpiirto-ohjelmaan. Ideaalisoidussa kuvaajassa käytetään yhdistä pisteet toimintoa kuvaajan saamiseksi.