FYS 3 - Sähkö

1 Tasavirta

Virtapiiri
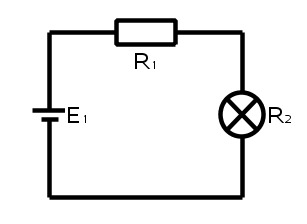
  • Sähkölaitteitteet perustuvat virtapiireihin.
  • Virtapiiri tarvitsee toimiakseen jännitelähteen (esim. paristo), joka saa aikaiseksi sähkövirran.
  • Virtapiirejä havainnollistetaan kytkentäkaavioilla.
  • Virtapiirin yksinkertaisimmat komponentit ovat: tasajännitelähde, lamppu, vastus, virtamittari, jännitemittari ja kytkin.
  • Virtapiiri on avoin, jos sähkö ei pääse kulkemaan siitä. Suljetussa piirissä kulkee virta.
  • Sähkövirta kulkee plus navasti miinus napaan. Elektronit kulkevat vastakkaiseen suuntaan.
  • Tasavirta ja vaihtovirta. Symbolit.
Sähkövirran mikroskooppinen malli
  • Sähkövirta on varattujen hiukkasten (yleensä elektronien) liikettä.
  • Sähkövirta on mahdollista vain johtavassa aineessa (eli johteissa), kuten useimmissa metalleissa.
  • Johteissa on vapaita varauksenkuljettajia (elektroneja).
  • Vapaat elektronit ovat jatkuvasti sattumanvaraisessa liikkeessä (lämpöliike) johteen sisällä. Jos johteeseen on kytketty jännite, elektronit kulkevat keskimäärin vähän enemmän plus napaa kuin miinus napaa kohti. Tätä kutsutaan sähkövirraksi.
  • Elektronit törmäilevät jatkuvasti johteen atomeihin ja luovuttavat liike-energiaansa. Tälllä tavoin esim. pariston sähköenergia muuttuu johteen lämpöenergiaksi.
  • Sähkövirta I, [I] = A (ampeeri)

​[[$$ I = \frac{\Delta Q}{\Delta t} $$]]​

Sähkövirran mittamiinen
  • Ampeerimittari (A), kytketään sarjaan komponentin kanssa. 
  • Virta kulkee mittarin plusnavasta miinusnapaan.
  • Mittarin resistanssi on hyvin pieni.
Aine ja säteily
  • Liikkeessä olevat varaukset lähettävät ympärilleen aina sähkömagneettista säteilyä.
  • Kaikki aine koostuu varatuista hiukkasista, jotka ovat lämpöliikkeessä.
  • Tästä seuraa, että kaikki aine säteilee aina sähkömagneettista säteilyä, jota kutsutaan lämpösäteilyksi.
  • Jos aineessa lisäksi kulkee sähkövirtoja, säteilee aine enemmän ja saattaa lähettää muutakin kuin lämpösäteilyä.
Sähkövirran vaikutuksia
  • Säteilyvaikutus, esim. lämpö ja valo.
  • Kemialliset vaikutukset, kuten akun lataaminen, galvanointi ja kemialliset reaktiot.
  • Magneettiset vaikutukset, esim. sähkömagneetti.
Kirchhoffin I laki
  • IDEA: Sähkövirta ei häviä mihinkään virtapiirissä: jokaiseen risteyskohtaan saapuvan ja lähtevän virran määrä on sama.
  • Kuva

​[[$$ I_1+I_2=I_3+I_4+I_5 $$]]​

Tehtäviä
  • Virtapiirin piirtäminen nspiren widgetillä (jos käytössä abitissa). linkki blogiin
  • Piirtäminen muilla välineillä.


  • Virtapiirin rakentaminen komponenteista ja virran mittaaminen virtamittarilla.
  • Virtalaskut K1-lailla.
  • Virtojen suuruuden arviointi eri haaroissa.
  • Palaako lamppu vai ei eri haaroissa, kytkimien kera.
  • Varauksen muutoksen delta Q mittaaminen t,I-koordinaatistosta graafisella integraalilla.
Linkit

2 Tasajännite

Jännite
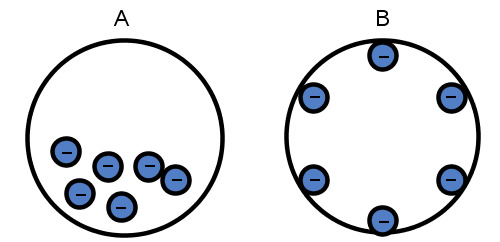
  • Jännite johtuu siitä, että varaukset ovat jakautuneet epätasaisesti virtapiirissä. Mitä suuremmat ovat varauserot, sitä suurempi on jännite.
  • Virta syntyy siitä, että varauserojen välinen jännite pyrkii tasoittumaan. (Siten, että johteen sisällä jänniteeksi tulee nolla.)


  • Jännitelähde on sellainen komponentti, joka tuottaa jatkuvan jännitteen, eikä varauserot pääse tasoittumaan koskaan.
  • Jännitteen symboli on U ja yksikkö V (Voltti).
  • Mitattaessa virtapiirin jännite-eroja jännitetä kutsutaan jännitehäviöksi.
Erilaiset jännitelähteet
  • Akku, paristo, aurinkokenno, vetykenno.
  • Tasajännite vai vaihtojännite.
  • Lähdejännite on akun napojen välinen jännite.
  • Akkua kutsutaan kuormitetuksi, kun se on kytketty johonkin kuormaan, eli sählaitteeseen.
  • Kuormitetun akun navoista mitattu jännite (napajännite) on pienempi kuin kuormittamattoman. Tämä johtuu siitä, että myös akun sisällä on virran kulkua vastustavia voimia, eli vastus.
Jännitteen mittaaminen
  • Jännitemittari kytketään tutkittavan komponentin rinnalle.
  • Mittarin plusnapa yhdistetään puolelle, jossa on pariston plusnapa.
  • Mittari kertoo komponentin päiden välillä olevan jännite-eron. Tätä kutsutaan jännitehäviöksi (koska jännite pienenee sen verran komponentissa).
  • Mittarin kautta kulkeva virta on mahdollisimman pieni, eli mittarin resistanssi on suuri.
Sähköinen pari
  • Koostuu kahdesta eri aineesta, joiden kemiallinen ominaisuus, jota kutsutaan elektronegatiivisuudeksi poikkeaa toisistaan.
  • Poikkeama synnyttää jänniteen ja saa aikaiseksi sähkövirran aineiden välillä.

Tehtäviä
  • Jännitemittarin kytkeminen ja jännitteen mittaaminen.
  • Jännitteen päätteleminen virtapiirissä.
  • Sähköisen parin jännitteen laskeminen.
Linkit

3 Ohmin laki ja resistanssi

Resistanssi
  • Resistanssi kuvaa kappalleen tai virtapiirin komponentin kykyä vastustaa virran kulkua.
  • Mitä suurempi resistanssi, sitä pienempi sähkövirta.
  • Resistanssin symboli on R ja yksikkö [[$ \Omega $]]​ (Ohm).
  • Sähköinen energia muuttuu vastuksessa lämpöenergiaksi. Eli elektronien virtaus muuttuu vastuksen molekyylien lämpöliikkeeksi.

Ohmin laki
  • Ohmin laki kuvaa virran ja jännitteen välistä riippuvuutta yksinkertaisessa virtapiirissä.
  • Riippuvuus on lineaarinen, eli jännitteen kasvaessa virta kasvaa samassa suhteessa.
  • Ohmin laki:
​[[$$ U = RI $$]]​


Hehkulampun U(I) kuvaaja
  • Huom! Ohmin laki pätee vain, jos virtapiirin lämpötila pysyy vakiona!
  • Jos vastuksen lämpötila pääsee nousemaan, myös vastuksen resistanssi yleensä kasvaa.
  • Tämä johtuu vastuksen molekyylien suuremmasta lämpöliikkeestä, mikä yleensä haittaa elektronien virtausta. 
  • Hehkulampun U(I)-kuvaaja ei ole lineaarinen, virta kasvu hidastuu jännitteen kasvaessa.
Muuta
  • Säätövastus, säädettävä jännitelähde
Tehtäviä
  • Komponentin resistanssin mittaaminen säädettävän jännitelähteen/säätövastuksen, virtamittarin ja jännitemittarin avulla.
  • Lineaarinen malli ja lineaarisen mallin sovittaminen datapisteikköön.
  • Virtapiirin laskeminen Ohmin lain avulla.
  • Hehkulangan U(I)-kuvaajan piirtäminen.

4 Resistanssiin vaikuttavat tekijät

Resistanssiin vaikuttavat tekijät
  • Resistiivisyys [[$ \rho $]]​ kuvaa aineen ominaisuutta vastustaa sähkövirran kulkua. Yksikkö on [[$ \Omega m $]]​.
  • Sähköjohdon resistanssi voidaan laskea alla olevalla kaavalla, jossa l on johtimen pituus ja A on johtimen poikkipinta-ala.

​[[$$ R = \frac {\rho l}{A} $$]]​
  • Lämpötila noustessa resistanssi yleensä kasvaa (PTC-vastukset).
  • Poikkeuksena ovat NTP-vastukset joiden resistanssi laskee lämpötilan noustessa.
  • Pystytään valmistamaan myös vastuksia, joiden resistanssi riippuu siihen kohdistuvan sähkömagneettisen säteilyn, kuten valon määrästä.
  • Suprajohtavuus
Tehtäviä
  • Resistanssin laskeminen ja sähköjohdon resistanssin kaavan käyttäminen.
  • Tutustu erilaisiin vastustyyppeihin

5 Potentiaali virtapiirissä

Potentiaali
  • Potentiaali ilmaisee tarkasteltavan pisteen jännitettä suhteessa valittuun nollapisteeseen.
  • Potentiaali auttaa jännitteiden laskemisessa.
  • Sähköistä potentiaalia voidaan verrata mekaaniseen potentiaalienergiaan.
  • Potentiaalin symboli on V ja yksikkö V (Voltti).
Potentiaalin määrittäminen
  • Valitaan joku piste virtapiiristä nollapotentiaaliksi.
  • Pistettä kutsutaan maadoituspisteeksi ja sen potentiaali on nolla.
  • Muiden pisteiden potentiaalit saadaan mittaamalla jännite suhteessa nollapotentiaaliin.
Jännitteen määrittäminen potentiaalin avulla
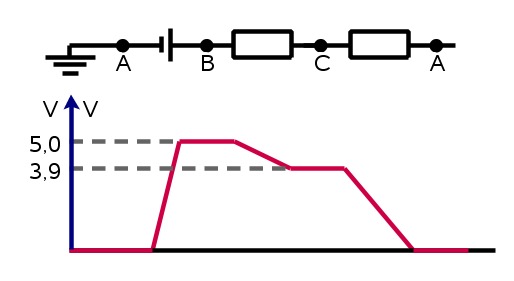
  • Pisteiden B ja A välinen jännite saadaan niiden potentiaalieron avulla.
​[[$$ U_{BA} = V_B - V_A $$]]​
  • Potentiaali ja jännite ovat käsitteinä hyvin lähellä toisiaan. Ainoa ero on, että potentiaalisissa jännite-eroa mitataan aina suhteessa nollapisteeseen, eli maahan.
Potentiaalikäyrä
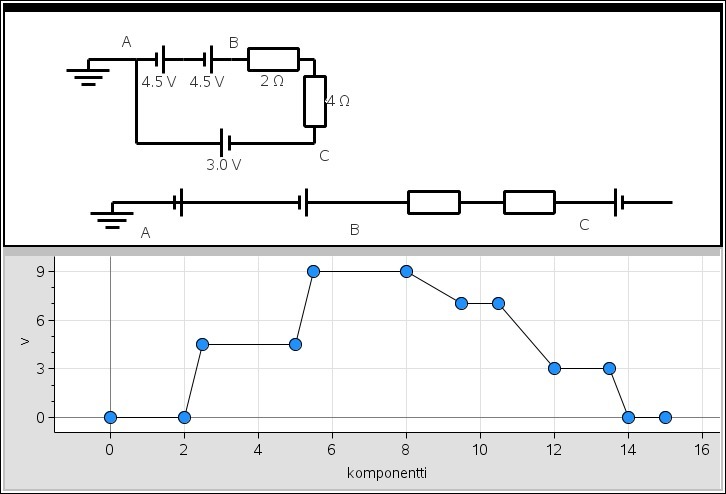
  • Potentiaalikäyrä on graafinen apuväline, jonka tarkoitus on havainnollistaa virtasilmukan toimintaa.
  • Potentiaali kasvaa kuljettaessa jännitelähteen yli ja vähenee vastuksen tai lampun kohdalla jännitehäviön verran.
  • Huom! Jos jännitelähde on kytketty virran kulkusuuntaa vastaan, jännite laskee sen kohdalla.



Kirchhoffin toinen laki
  • Suljetun virtasilmukan potentiaalimuutosten summa on nolla. [[$ \Sigma \Delta V = 0 $]]​
  • Kaavaa on helppo havainnollistaa potentiaalikäyrän avulla.
  • Käytetään virtapiirien matemaattisessa ratkaisemisessa.
Tehtäviä
  • Potentiaalikäyrän piirtäminen (tiNspire) ja tulkitseminen.

  • Virtapiirin potentiaalien, jänniteiden ja virtojen laskeminen.
  • Maadoituksen vaikuttaminen virtapiirin käyttäytymiseen.

6 Vastusten sarja- ja rinnakkaiskytkentä

Vastusten kytkennät
  • Vastusten tehtävä virtapiirissä on säädellä virran kulkua. Sopivalla vastuksella tai vastusten yhdistelmällä saadaan piiriin juuri sopivanlainen virta aikaiseksi.
  • Säätövastus on komponentti, jonka vastus voidaan säätää sopivaksi. (Esim. ruuvia ruuvaamalla vastuksen kannessa).
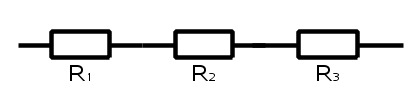
  • Vastuksia voidaan yhdistellä kahdella eri tavalla sopivan kokonaisvastuksen saamiseksi. Niitä voidaan kytkeä sarjaan tai rinnan.
  • Sarjaan kytkennässä sama virta kulkee kaikkien vastusten läpi.

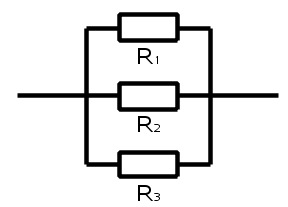
  • Rinnakkainkytkennässä virta jakautuu siten, että pienimmän vastuksen läpi kulkee eniten ja suurimman vähiten virtaa.

Resistanssin laskeminen
  • Kun vastukset ovat kytketty sarjaan, kokonaisvastus saadaan laskemalla resistanssit yhteen:
​[[$$ R = R_1 + R_2 + R_3 $$]]​
  • Kun vastukset on kytketty rinnan pienenee (koska virralla on enemmän reittejä) ja resistanssi saadaan kaavasta

[[$$ \frac {1}{R} = \frac {1}{R_1} + \frac {1}{R_2} + \frac {1}{R_3} $$]]​
  • Kokonaisvastusta kutsutaan toisinaan ekvivalenttivastukseksi.
Tehtäviä
  • Kokonaisvastuksen laskeminen sarjakytkennässä ja rinnakkaiskytkennässä.
  • Kokonaisvastuksen laskeminen tilanteessa, jossa on sekä sarjaan että rinnan kytkettyjä vastuksia.
  • Virran suuruuden arviointi ja laskeminen rinnakkaiskytkennän eri haaroissa.

7 Sähkölaitteen teho ja energian kulutus

Sähköteho
  • Yleisesti teholla tarkoitetaan energian muuttumista muodosta toiseen tai siirtymistä kohteesta toiseen.
  • Esimerkiksi polttomoottorissa polttoaineen kemiallinen energia muuttuu auton liike-energiaksi.
  • Huom! Energia menee aina myös hukkaan (esim. polttomoottorissa lämpöenergiaksi), pitää olla siis tarkka puhutaanko hyötytehosta vai kokonaistehosta.
  • Sähköteho tarkoittaa laitteen kykyä muuttaa sähköenergia toiseen muotoon, esim. lämpöenergiaksi tai liike-energiaksi. Yleensä tällöin tarkoitetaan kokonaistehoa.
  • Teho saadaan Joulen lain avulla:
​[[$$ P = UI $$]]​

tai toisessa muodossa:

​[[$$ P = RI^2 $$]]​

Sähkölaitteen muuntama energia
  • Sähkölaiteen tuottama energia saadaan kertomalla teho ajalla:
​[[$$ E = Pt $$]]​
  • Joulen (J) lisäksi yleinen sähköenergian yksikkö on kilowattitunti (kWh).
  • Esimerkiksi sähkölaitokset laskuttavat energiaa käytettyen kilowattituntien mukaan (johon lisätään vielä sähkön siirtomaksu).
Tehtäviä
  • Tehon laskeminen Joulen lain avulla.
  • Energian laskeminen.
  • Energian yksikön muuntaminen jouleista kilowattitunneiksi.
  • Energian graafinen integrointi t,P-koorditaatistossa.
  • Sähkön kulutuksen arviointi ja kustannusten arviointi.
  • Sähkölaitteiden merkintöjen ymmärtäminen.

8 Paristojen kuormituskäyrä ja paristojen kytkennät

Pariston sisäinen vastus
  • Paristojen sisäinen rakenne rajoittaa virran kulkua. Tätä ominaisuutta kutsutaan sisäiseksi vastukseksi ja merkitään Rs.
  • Sisäinen vastus riippuu pariston tyypistä ja pariston iästä. Pitkäänkäytetyn pariston sisäinen vastus on suuri.
  • Kuormittamattoman pariston jännitetettä kutsutaan lähdejännitteeksi (E).
  • Kun paristo syöttää virtaa virtapiiriin osa jännitteestä häviää sisäiseen vastukseen. Virtapiirille käyttöön jäävää jännitettä kutsutaan napajännitteeksi (U) ja se on aina pienempi kuin lähdejännite.
​[[$$ U = E - R_s I $$]]​

Kuormituskäyrä
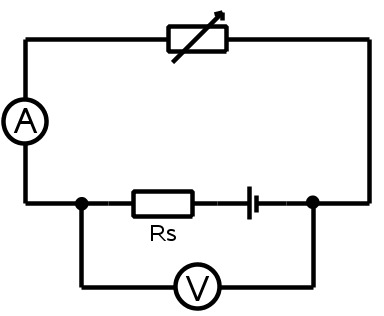
  • Pariston sisäinen vastus pystytään laskemaan yksinkertaisen mittausasetelman avulla. Paristo kytketään säätövastukseen, jolla säädellään sen kautta kulkevaa virtaa.
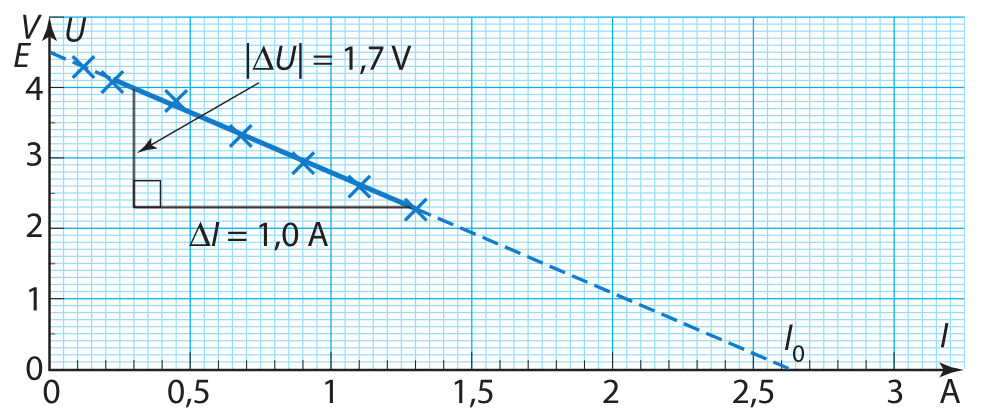
  • Kun napajännitteitä mitataan eri virran arvoilla, mittaustuloksista syntyy kuvaaja, jota kutsutaan kuormituskäyräksi (vaikka sen onkin suora).
  • Kuormituskäyrä noudattaa ylläolevaa kaavaa ja sisäinen vastus saadaan suoran kulmakertoimesta.
​[[$$ R_s = \frac{\Delta U}{\Delta I} $$]]​
  • Kuva mittausasetelmasta:

  • Kuormituskäyrä:

  • Kuvaajasta nähdään, että napajännite pienenee, kun piirissä kulkeva virta kasvaa. Eli mitä suurempaa tehoa paristosta yritetään ottaa, sitä enemmän tehosta kuluu pariston itsensä lämpenemiseen (tai muihin sisäisiin muutoksiin).
  • Kuvaajasta voidaan selvittää myös paristosta saatava maksimaalinen virta I0. Tämä saadaan silloin kun paristo on oikosulussa ja virtaa kutsutaan oikosulkuvirraksi.
Paristojen kytkennät
  • Sarjaankytkenässä paristojen jännite on niiden yhteenlaskettu jännite. Esim. neljästä sarjaankytketystä sormiparistosta saadaan noin 6 voltin lähdejännite.
  • Haittapuolena sarjaankytkennässä on se, että myös sisäinen jännite summaantuu.
  • Rinnankytkettyjen paristojen lähdejännite on sama kuin yksittäisen pariston lähdejännite, eli jännitettä ei saada nostettua.
  • Hyvä puoli on se, että rinnankytkennässä sisäisen vastuksen merkitys pienenee ja paristojen energia saadaan paremmin hyödynnettyä. Paristot myös kestävät kauemmin.
  • Huom! Rinnankytkennässä paristojen lähdejännite on oltava sama! Muuten paristojen välille syntyy sähkövirta ja paristot kuluvat vaikkei sähkölaitetta olisi kytketty päälle. 
Tehtäviä
  • Selvitä lähdejännitteen ja napajännitteen ero.
  • Napajännitteen laskeminen suljetussa virtapiirissä.
  • Piirrä kytkentäkaavio, jonka avulla voit mitata pariston sisäisen vastuksen.
  • Kuormituskäyrän piirtäminen data-aineiston avulla.
  • Sisäisen vastuksen laskeminen kuormituskäyrältä.
  • Oikosulkuvirran selvittäminen kuormituskäyrältä.
  • Piirrä paristojen rinnankytkentä ja sarjaankytkentä.
  • Laske rinnankytketyn paristokokonaisuuden sisäinen vastus.