Vastusten kytkennät

• Vastusten tehtävä virtapiirissä on säädellä virran kulkua. Sopivalla vastuksella tai vastusten yhdistelmällä saadaan piiriin juuri sopivanlainen virta aikaiseksi.
• Säätövastus on komponentti, jonka vastus voidaan säätää sopivaksi. (Esim. ruuvia ruuvaamalla vastuksen kannessa).
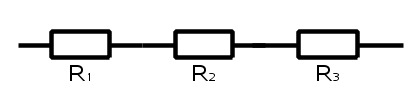
• Vastuksia voidaan yhdistellä kahdella eri tavalla sopivan kokonaisvastuksen saamiseksi. Niitä voidaan kytkeä sarjaan tai rinnan.
• Sarjaan kytkennässä sama virta kulkee kaikkien vastusten läpi.

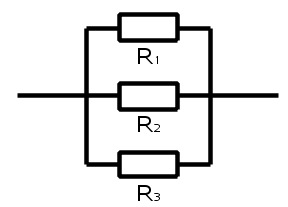
• Rinnakkainkytkennässä virta jakautuu siten, että pienimmän vastuksen läpi kulkee eniten ja suurimman vähiten virtaa.

Resistanssin laskeminen

• Kun vastukset ovat kytketty sarjaan, kokonaisvastus saadaan laskemalla resistanssit yhteen:

​[[$$ R = R_1 + R_2 + R_3 $$]]​

• Kun vastukset on kytketty rinnan pienenee (koska virralla on enemmän reittejä) ja resistanssi saadaan kaavasta

[[$$ \frac {1}{R} = \frac {1}{R_1} + \frac {1}{R_2} + \frac {1}{R_3} $$]]​

• Kokonaisvastusta kutsutaan toisinaan ekvivalenttivastukseksi.

Tehtäviä

• Kokonaisvastuksen laskeminen sarjakytkennässä ja rinnakkaiskytkennässä.
• Kokonaisvastuksen laskeminen tilanteessa, jossa on sekä sarjaan että rinnan kytkettyjä vastuksia.
• Virran suuruuden arviointi ja laskeminen rinnakkaiskytkennän eri haaroissa.