8. Suora johdin ja käämi ulkoisessa magneettikentässä
8-1
a) kenttäviivojen suuntaan
b) kohtisuoraan magneettikenttää vastaan
8-2
a) Ylöspäin
b) Vasemmalle
c) Oikea-alakulmaan
d) Vasemmalle
8-5



 b)
b)




8-6




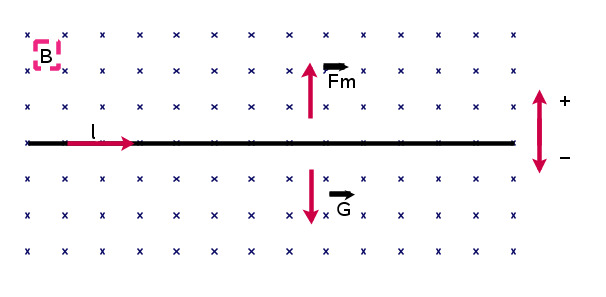
8-8
Koska johdin pysyy paikallaan ,
, 









 8-9
8-9
a)
b)





 , jossa
, jossa  on alumiinin tiheys.
on alumiinin tiheys.
%5E2%5Ccdot9%7B%2C%7D81%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7B0%7B%2C%7D56T%7D%5Capprox37mA)
 , kun
, kun  on tyhjiön permeabiliteetti,
on tyhjiön permeabiliteetti,  ja
ja  ovat johtimessa kulkevat sähkövirrat, r on johdinten välinen etäisyys ja l virtajohtimien pituus.
ovat johtimessa kulkevat sähkövirrat, r on johdinten välinen etäisyys ja l virtajohtimien pituus.
%7D%7D%7B2%5Cpi%7D%5Ccdot%5Cfrac%7B2%7B%2C%7D5A%5Ccdot2%7B%2C%7D5A%7D%7B0%7B%2C%7D19m%7D%5Ccdot1%7B%2C%7D4m%5Capprox9%7B%2C%7D2%5Ccdot10%5E%7B-6%7DN)
a) kenttäviivojen suuntaan
b) kohtisuoraan magneettikenttää vastaan
8-2
a) Ylöspäin
b) Vasemmalle
c) Oikea-alakulmaan
d) Vasemmalle
8-5
a)
Magneettinen voima  on suurin, kun
on suurin, kun  eli kun α=90. Johdin on siis asetettava kohtisuoraan magneettikenttää vastaan,
eli kun α=90. Johdin on siis asetettava kohtisuoraan magneettikenttää vastaan,
Magneettivuon tiheys on
8-6
Magneettivuon tiheys on
8-8
Koska johdin pysyy paikallaan
johtimeen kohtistuva paino on samakuin magneettikentästä tuleva voima, eli
Paino lasketaan kaavalla
jossa
Koska halutaan saada sähkövirran suuruus,
Koska tehtävässä mainittiin, että johdin on kohtisuorassa kenttäviivojen vastaan,
Johtimen suunta on vasen-oikeasuunnassa, sähkövirran suunta on oikealle
a)

b)
Biotin-Savartin laen mukaan
Koska tässä me halutaan johtimessa kulkevan virran suuruus
Newtonin II lain mukaan on  eli
eli  . Kun suunta ylös valitaan positiiviseksi, skalaariyhtälö on
. Kun suunta ylös valitaan positiiviseksi, skalaariyhtälö on  , joka saadaan muotoon
, joka saadaan muotoon  eli
eli 
 . Johtimen massa voidaan kirjoittaa muotoon
. Johtimen massa voidaan kirjoittaa muotoon
Johdin on muodoltaan suora ympyrälieriö, joten sen tilavuus on
Johtimessa kulkevan sähkövirran suuruus on
8-10
a) Ampèren lain mukaan suora virtajohdin kohdistaa toiseen yhdensuuntaiseen virtajohtimeen voiman, jonka suuruus on
b)
Ksoka virtajohtimissa sähkövirrat kulkevat samaan suuntaan, johtimet vetävät toisiaan puoleensa. Virtajohtimiin kohdistuvat voimat ovat Newtonin III lain mukaan yhtä suuret ja vastakkaissuuntaiset. Voimien suuruudet ovat
Kommentit
Kirjaudu sisään lisätäksesi tähän kommentin