Oppilastyö

Työselostus: Tiheys (Valmis)

Työselostus: Tiheys

Johdanto

Työn tarkoitus oli esittää matemaattinen malli, joka kertoo, kuinka aineen massa ja tilavuus riippuvat toisistaan. Oli mitattava riisi, kaurahiutale ja sokeri, ja valitsin niistä riisin ja kaurahiutaleen.

Teoria

Tämän kokeen taustana on aine tiheyden kaava $\rho=\frac{m}{V}$ , jonka mukaan aineen tiheyttä saadaan massa jaettuna tilavuudella, ja se on tarkoittaa myös sitä, että aineen massa ja tilavuus ovat riippuvaisia toisistaan.

Mittalaitteet ja mittaukset

Kokeessa käytettiin mittalasia, vaakaa sekä tutkittavia aineita: riisiä ja kaurahiutaleitä. Ensimmäisenä asetiin mittalasia vaa’an päälle ja taaratiin vaaka. Toiseksi kaadettiin keitinlasilla pieni määrä (10 ml kerralla) riisiä mittalasiin, ja punnittiin sen painoa. Joka mittauksen jälkeen on merkitsevä ne mittatulokset taulukkoon. Sama prosessi toistuu. Lopuksi tyhjennettiin mittalasia ja toistettiin sitä sama prosessia vielä toisen aineen kanssa.

Mittalasi

Vaaka

Keitinlasi

Riisi

Kaurahiutaleet

Tulokset

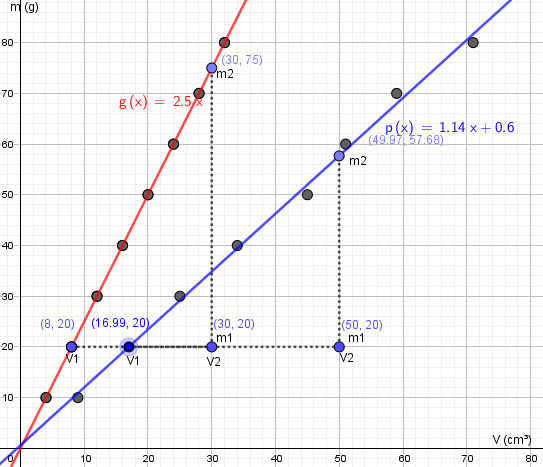
Mitattiin kahden aineen massa kohteilla 10ml, 20ml, 30ml, 40ml, 50ml, 60ml, 70ml ja 80ml, ja mittaaminen onnistui hyvin. Koetulosten ja geogebran avulla saatiin selville, että riisin tiheys on 1,14 g/cm³ ja kaurahiutale 2,5 g/cm³.

$\Delta x=\frac{\Delta m}{\Delta V}=\frac{m_2-m_1}{V_2-V_1}=\frac{75-20}{30-8}=2,5\ \frac{g}{cm^3}$

$\Delta x=\frac{\Delta m}{\Delta V}=\frac{m_2-m_1}{V_2-V_1}=1,141...\approx1,14\frac{g}{cm^3}$

Mittaustarkkuus ja virheen arviointi

Aine 1: Riisi
m (g)	V(cm³=ml)
9g	10ml
17g	20ml
25g	30ml
34g	40ml
45g	50ml
51g	60ml
59g	70ml
71g	80ml

Aine 2: Kaurahiutale
m (g)	V (cm³=ml)
4g	10ml
8g	20ml
12g	30ml
16g	40ml
20g	50ml
24g	60ml
28g	70ml
32g	80ml

Kokeessa käytetty yksikkö oli millilitra ja gramma, mutta niistä suurin virhe tekijä ei ole kumpikaan niistä, vaan se johtuu todennäköisesti epätarkasta kaatamisesta. Koska sekä riisi että kaurahiutaleet ovat vaikea kaataa tasaisesti ja samanvertaisesti mittalasiin. Toisaalta me huomattiin, kun sitä mittalasia heilutetiin kevyellä voimalla, sen lukema voi olla hyvin erilainen verrattuna ennen sitä heilumista. Joten mittaamisessa voi hyvinkin olla virheitä. Kokeessa yritettiin olla mahdollisimman tarkka, koska me haluttiin saada mahdollisimman tarkat mittatulokset, ensimmäisen aineen kanssa kävi vähä huonosti, mutta toisen kanssa eriomaisesti. Epätarkat tulokset voivat aiheuttaa kuvaajan piirtämiselle ongelmia, sillä niiden pisteiden paikat ovat epäsäännöllisesti luokiteltu kuvaajalle, mutta geogebra avusti meidät laskemisessa aika paljon.

Johtopäätökset

Johtopäätöksenä me saatiin mittauksien ja kuvaajan avulla, että aineen massa ja tilavuus ovat riippuvaisia toistaan, ja jakamalla massaa tilavuudella saadaan aineen tiehyttä. koska $\rho=\frac{m}{V}$ . Ollaan hyvin tyytyväisiä koetuloksista, mutta olisimme saanut vielä tarkemman tuloksen, jos me olisi mitannut noita mittauksia useamman kerran, silloin ne tulokset voivat olla vielä tarkempia kuin mitä meillä on nyt.

Lähteet

FY1 Fysiikka luonnontieteenä Sanomapro Heikki lehto, Jukka Maalampi Raimo Havukainen, Janna Leskinen
Google kuvahaku

1 kommenttia