Funktion kuvaaja

Kuvaajan [[$y=f(x)$]] avulla havainnollistetaan graafisesti, millä tavoin [[$y$]] riippuu muuttujasta [[$x$]].

Kuvaaja on pisteiden [[$(x,f(x))$]] joukko

  • Funktion kuvaaja saadaan piirrettyä, kun asetetaan [[$y = f(x)$]].
  • Käydään läpi kaikki määrittelyjoukkoon kuuluvat muuttujan [[$x$]] arvot ja lasketaan niitä vastaavat funktion arvot.
  • Piirretään muuttujan [[$x$]] kohdalle piste siihen y-akselin kohtaan, mikä vastaa funktion arvoa kohdassa [[$x$]].
  • Kuvaaja muodostuu siis pisteistä [[$(x,y)$]], joissa y-koordinaatti on funktion [[$f$]] arvo kohdassa [[$x$]].
  • Kuvaajan pisteet ovat muotoa [[$(x,f(x))$]].
Muista, että xy-koordinaatistossa vaaka-akseli muodostaa kaikki muuttujan [[$x$]] arvot ja y-arvo ilmoittaa paikan pystysuunnassa. Nolla pystysuunnassa tarkoittaa, että ollaan [[$x$]]-akselilla. Akseleiden nuolet ilmoittavat positiivisen suunnan: nuolen suuntaan liikuttaessa arvo kasvaa. Tapana on, että muuttuja on vaaka-akseli ja että riippuvaa suuretta kuvataan pystyakselille.

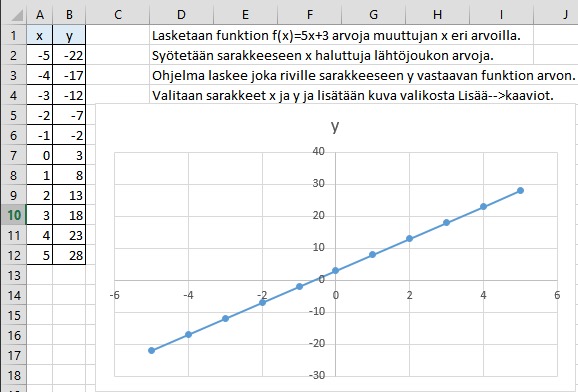
Kuvaajan piirto taulukkolaskentaohjelmalla

  • Luodaan muuttujasarake [[$x$]]
  • Lasketaan vastaavat funktion arvot sarakkeeseen [[$y$]]
  • Muodostetaan [[$x$]] ja [[$y$]] -sarakkeista graafi, eli piirretään pisteet xy-koordinaatistoon
​​

Kuvaajan piirto GeoGebralla

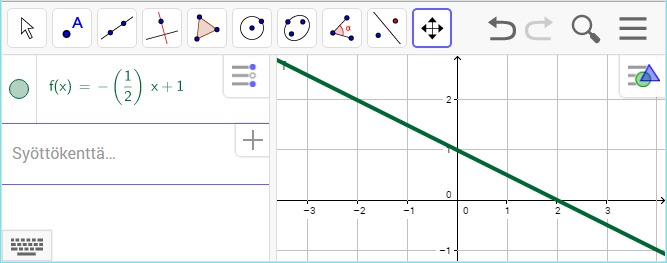
GeoGebra -ohjelma piirtää funktion kuvaajan, kun funktio kirjoitetaan syöttökenttään. Kokeile itse erilaisten funktioiden kuvaajien piirtoa osoitteessa: http://web.geogebra.org/#algebra. Voit muuttaa funktiota klikkaamalla syöttämäsi funktion lauseketta.

Kuvaajan tulkitseminen, kuvaajan [[$y=f(x)$]] piste [[$(x,y)$]]
on piste [[$\left(x,f(x)\right)$]]

  • muuttuja-akseli on [[$x$]]-akseli
  • funktion arvoakseli on [[$y$]]-akseli
Funktion kuvaajasta voidaan määrittää graafisesti funktion arvoja eri muuttujan arvoilla. Muuttujan arvoja kuvaa vaaka-akseli ja funktion arvoja kuvaa pystyakseli. Oheisen sovelman avulla voit harjoitella määrittämään funktion arvoja eri kohdissa [[$x$]]-akselia.

  • Selvitä yllä olevan sovelman avulla, mikä on lausekkeen [[$\frac{1}{8}\cdot 2^3$]] arvo.
  • Selvitä millä muuttujan [[$x$]] arvolla pätee [[$x=\frac{1}{8}\cdot x^3$]].