10. Geometric number sequences
Geometric number sequences
The sequence [[$ 1, 2, 4, 8, 16, 32,… $]] is an example of a geometric number sequence. In it, each term is obtained by multiplying the previous number by [[$ 2 $]]. Such a sequence, in which the term is obtained from the former by multiplying it by the same constant, is called a geometric sequence.
Consider the representation of the general term [[$ a_n $]] in a geometric sequence, using the first term in the sequence [[$ a_1 $]] and the constant [[$ q $]].
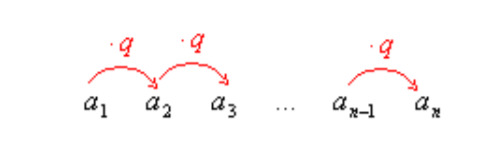
[[$ \quad \begin{align*} a_2 &= a_1 q \ \\ a_3 &= a_2 q = a_1 qq = a_1 q^2 \ \\ a_4 &= a_3 q = a_1 qqq = a_1 q^3 \ \\ a_n &= a_1 q^{n-1} \end{align*} $]]
In a geometric number sequence, the ratio of two consecutive terms is constant.
The general term for a geometric sequence is [[$ a_n = a_1q^{n - 1}, $]]where [[$ a_1 $]] is the first term and [[$ q $]] is the ratio.
Example 1
Bacteria multiply by dividing in two. Some bacteria initially are [[$ 10 $]] and their number doubles every hour. The number of bacteria can be described with the following number sequence:
[[$ 10, 20, 40, 80, 160, … $]]
This is a geometric number sequence with the first term of [[$ a_1 = 10 $]] and a ratio of [[$ q = 2 $]].
a) Let's form a general term for the sequence
[[$ a_n = 10 \cdot 2 ^{n - 1} $]]
b) Calculate the number of bacteria after [[$ 20 $]] hours
[[$ a_{20} = 10 \cdot 2 ^{20 - 1} = 5 242 880 $]]
Example 2
Henry deposited [[$ 1500 $]] QAR in his account. The annual interest rate on the account was [[$ 3,0\% $]], so the deposit will increase by [[$ 1,03 $]] times each year. The amount of money in the account can be described as a geometric sequence:
[[$ 1500 \: \text {QAR} \cdot 1,03 $]], [[$ 1500 \: \text {QAR}\cdot 1,03^2 $]][[$ 1500 \: \text {QAR} \cdot 1,03^3 $]],[[$ 1500 \: \text {QAR} \cdot 1,03^4 $]], ... , [[$ 1500 \: \text {QAR} \cdot 1,03^n $]]
The first term in the sequence is [[$ a_1 = 1500 \: \text {QAR} \cdot 1,03 = 1545 \: \text {QAR} $]], and the ratio of the sequence is [[$ q = 1,03 $]].
a) Let's form a general term for the sequence.
[[$ a_n = 14514 \: \text {QAR} \cdot 1,03 ^{n - 1} $]]
b) Let’s calculate how much savings Henry has in 10 years.
[[$ a_{10} = 14514 \: \text {QAR} \cdot 1,03 ^{10 - 1} = 2015,87 \: \text {QAR} $]]
Exercises
Basic exercises
Applied exercises
Challenging exercises
1/10. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.