4.4 Aritmeettinen summa
Laskettaessa yhteen tietty määrä peräkkäisiä aritmeettisen lukujonon jäseniä saadaan aritmeettisen lukujonon summa. Summaa merkitään lyhenteellä Sn, missä S tarkoittaa summaa ja alaindeksi n on summattavien termien määrä.
Kokonaisluvut 1, 2, 3,...ovat osa aritmeettista lukujonoa. Merkintä S5 tarkoittaa siis laskua
S5 =1 + 2 + 3 + 4 + 5 = 15.
Aritmeettinen summa saadaan valmiina ratkaisukaavan avulla.
Kaavassa
------------------------------------------------------------------------------------------------------------------------------------------
Summamerkintänä voidaan käyttää myös kreikkalaista merkkiä Σ (sigma), joka tarkoittaa summaa. Lisäksi on tunnettava aritmeettisen lukujonon yleisen jäsenen lause.
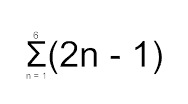
Tarkoittaa siis summaa kuudelle ensimmäiselle termille lukujonossa, jonka yleinen jäsen saadaan kaavalla an = 2n - 1. Lukunon ensimmäinen jäsen a1 = 1 ja kuudes jäsen a6 = 11.
Kaavaan sijoitettuna summaksi saadaan Σ = 6 · [(1 + 11) : 2] = 6 · 6 = 36
Summan voisi esittää myös muodossa 1 + 3 + 5 + 7 + 9 + 11 = 36
Summalausekkeet ovat käytännöllisiä silloin, kun yhteenlaskettavia on suuri määrä.
Esimerkki. Laske summa
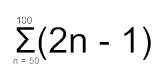
------------------------------------------------------------------------------------------------------------------------------------------
Kokonaisluvut 1, 2, 3,...ovat osa aritmeettista lukujonoa. Merkintä S5 tarkoittaa siis laskua
S5 =1 + 2 + 3 + 4 + 5 = 15.
Aritmeettinen summa saadaan valmiina ratkaisukaavan avulla.
Kaavassa
- n on yhteenlaskettavien lukumäärä
- a1 on ensimmäinen yhteenlaskettava
- an on viimeinen yhteenlaskettava
------------------------------------------------------------------------------------------------------------------------------------------
Summamerkintänä voidaan käyttää myös kreikkalaista merkkiä Σ (sigma), joka tarkoittaa summaa. Lisäksi on tunnettava aritmeettisen lukujonon yleisen jäsenen lause.
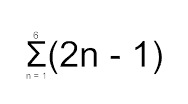
Tarkoittaa siis summaa kuudelle ensimmäiselle termille lukujonossa, jonka yleinen jäsen saadaan kaavalla an = 2n - 1. Lukunon ensimmäinen jäsen a1 = 1 ja kuudes jäsen a6 = 11.
Kaavaan sijoitettuna summaksi saadaan Σ = 6 · [(1 + 11) : 2] = 6 · 6 = 36
Summan voisi esittää myös muodossa 1 + 3 + 5 + 7 + 9 + 11 = 36
Summalausekkeet ovat käytännöllisiä silloin, kun yhteenlaskettavia on suuri määrä.
Esimerkki. Laske summa
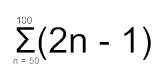
------------------------------------------------------------------------------------------------------------------------------------------
