Korko

Korko on rahasta tietyltä ajalta maksettava korvaus. Korko on sitä korkeampi mitä riskipitoisempi laina on kyseessä.

Yksinkertainen korko

Korkoa kertyy lainapääomalle. Kertyvä korko on suoraan verrannollinen laina-ajan pituuteen.

Korko lasketaan kaavasta:

[[$ R = \frac{k \cdot i \cdot t}{100 \cdot 365} $]]​

missä

k on jäljellä oleva pääoma

i on vuotuinen korko

t on laina-aika päivinä

Korkopäivät

Korkoaika ilmoitetaan yleensä kahden päivämäärän avulla, esimerkiksi 1.2. – 15.6.2016. Korkoajan ensimmäiseltä päivältä ei makseta korkoa, mutta viimeiseltä maksetaan. Korkopäivien lukumäärä voidaan laskea kahdella eri tavalla:

• jokaisessa kuukaudessa on 30 päivää
• todellisten kalenteripäivien mukaan

Korkoaika vuosina

Laskuissa korkoaika ilmoitetaan vuosina. Korkoaika merkitään murtolukuna, joka kertoo kuinka suuri osa vuodesta korkopäivät ovat. Käytössä on kolme eri koronlaskutapaa:

• Korkopäivät lasketaan todellisten päivien mukaan ja vuodessa on 365 päivää
• Korkopäivät lasketaan todellisten päivien mukaan ja vuodessa on 360 päivää
• Jokaisessa kuukaudessa on 30 päivää ja vuodessa on 360 päivää

Korkoa korolle

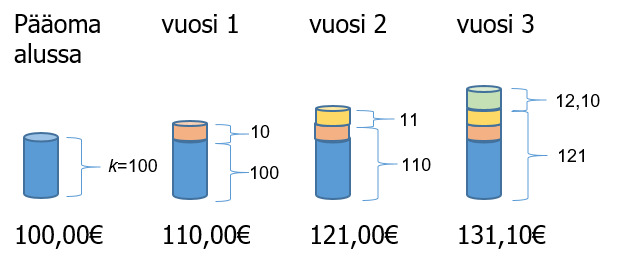
Korkoa korolle -laskelmissa ensimmäisen vuoden jälkeen lasketaan korkoa, paitsi alkuperäiselle pääomalle, myös edellisinä vuotena kertyneelle korolle. Tällöin korko on joka vuosi hieman edellistä suurempi, ja aikaa myöten se kasvaa eksponentiaalisesti hyvinkin suureksi.

Sijoitettaessa pääoma k vuosikorolla i (prosenttia), sijoitus korkoineen K ensimmäisen vuoden lopussa eli toisen vuoden alussa on , esimerkiksi 100 € sijoitus 10 % korolla on tällöin kasvanut

[[$$ 100 € \cdot (1+\frac{10}{100}) = 100 € + 10 € = 110 € $$]]​
, jos tämä pääoma kasvaa korkoa vielä vuoden saadaan

[[$$ 110 € \cdot (1+\frac{10}{100}) = 110 € + 11 € = 121 € $$]]​

, kolmannen vuoden

[[$$ 121 € \cdot (1+\frac{10}{100}) = 121 € + 12,1 € = 133,10 € $$]]​

, jne.

Yleinen korkoa korolle kaava on

[[$$ K = k \cdot ( 1 + \frac{i}{100})^{n} $$]]​

jossa n on vuosien lukumäärä, k on pääoma, K on kasvanut pääoma ja i on korko prosentteina.

Viivästyskorko

Viivästyskorko on korkoa jota joudutaan maksamaan kun maksu maksetaan eräpäivän jälkeen, eli myöhässä.

Viivästyskorko lasketaan kaavalla

[[$$ korko = \frac{korkoprosentti \cdot viivästyspäivien lukumäärä \cdot laskun summa}{100 \cdot 360} $$]]​

Tehtäviä:

Laske Excelillä, oikea vastaus sulkeissa:

Korkoaika on 1.1. – 31.3. Montako korkopäivää aikavälillä on:

• 1. Vuonna 2011? (89)
  2. Vuonna 2016? (90)
  3. Vuonna 2018? (89)
  4. Vuonna 2020? (90)
• Korkoaika on 1.1.2016 – 31.5.2016, lainattu pääoma on 1200 € ja korko on 4,7%. Käytetään todelliset/365-laskentatapaa. Laske:
  1. Montako korkopäivää aikavälillä on? (151)
  2. Paljonko korko on euroina? (23,33 €)
• Entäpä jos lasketaan samoilla arvoilla, mutta käytetään 30/360-laskentatapaa?
  1. Montako korkopäivää aikavälillä on? (150)
  2. Paljonko korko on euroina? (23,50 €)
• Paljonko on viivästyskorko jos laskun summa on 1300 €, viivästyskorko 7 %, eräpäivä 1.12.2016 ja maksat sen
  1. 12.12.2016? (2,78 €)
  2. 31.1.2017? (15,42 €)
• Talletat tilille 30 000 €, vuotuinen korko on 7 %. Paljonko tilillä on rahaa:
  1. Kolmen vuoden päästä? (36 751,29 €)
  2. 10 vuoden päästä? (59 014,54 €)