Vektoreiden yhteen- ja vähennyslasku

Vektoreiden yhteenlasku tarkoittaa, että siirtymät asetetaan peräkkäin. Esimerkiksi summa [[$\bar a + \bar b$]] tarkoittaa siirtymää, joka syntyy kun ensin siirrytään vektorin [[$\bar a$]] siirtymä ja sen jälkeen vektorin [[$\bar b$]] siirtymä.
Voidaan osoittaa, että
[[$\bar a +\bar b = \bar b + \bar a$]]

Negatiivinen siirtymä tarkoittaa, että vektoria kuljetaan lopusta alkuun, siis nuolen osoittamaa suuntaa vastaan. Vektorin vähentäminen toisesta vektorista on sama asia kuin vastavektorin lisääminen:
[[$\bar a -\bar b = \bar a + (-\bar b)$]]

​Yllä voit tutkia, kuinka peräkkäin asetellut vektorit esitetään summalausekkeilla. Kokeile onnistutko rakentelemaan lausekkeet:
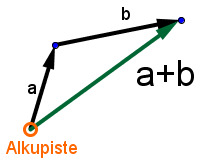
[[$\bar a + \bar b $]], [[$\bar a - \bar b $]], [[$\bar b + \bar a $]], [[$\bar b - \bar a $]], [[$-\bar b - \bar a $]], [[$-\bar b + \bar a $]], [[$-\bar a + \bar b $]], [[$-\bar a - \bar b $]]