Kevät 2021
Osa 2: 15 pisteen tehtävät

2.1 Piirretään GeoGebralla mittaustulokset ja sovitetaan pisteisiin splini-funktiolla sovitus.

2.2
Luetaan kuvaajalta GeoGebran avulla aika, kun paikka on 75 m:

Eli 75 m väliaika oli n. 7,7 s
2.3
Havaitaan kuvaajan olevan lineaarinen 60 m 100 metriin: Ekstrapoloidaan lineaarista osaa 200 metriin asti:

Kuvaajalta voidaan lukea näin juostun m200 m loppuajaksi 18,5 s









Voimakuvio B kuvaa parhaiten tilannetta.
F1 = Ilmanvastus
F3 = Takapyörän kitka
F6 = Takapyörään kohdistuva tukivoima
F7 = Etupyörään kohdistuva tukivoima
F8 = Pyörän ja pyöräilijän paino

Voimakuvio C kuvaa parhaiten tilannetta.
F1 = Istuimen lapseen kohdistama tukivoima
F3 = Lapsen paino
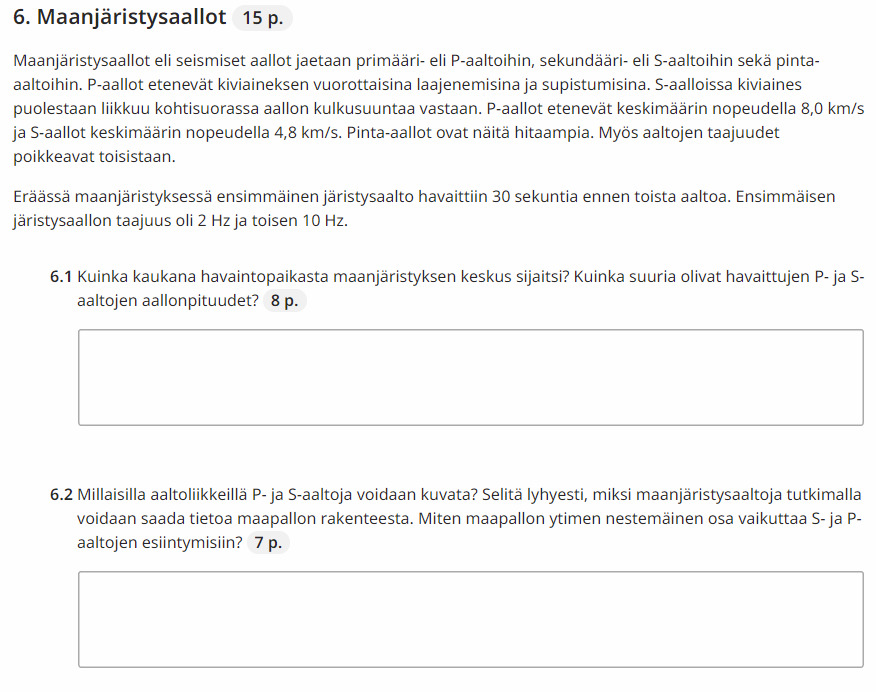
6.1.
Merkitään etäisyyttä x. Ensimmäisenä havaitaan P-aalto ja toisena S-aalto.
P-aalto on kulkenut matkan x ajassa tP nopeudella vP, joten
[[$ t_P=\frac{x}{v_P} $]]
Vastaavasti S-aalto
[[$ t_S=\frac{x}{v_S} $]]
Aikaero
[[$ \Delta t=t_S-t_P= \frac{x}{v_S}-\frac{x}{v_P}=x\left(\frac{1}{v_S}-\frac{1}{v_P}\right) $]], josta
[[$ x=\frac{\Delta t}{\frac{1}{v_S}-\frac{1}{v_P}} =\frac{30 \text{s}}{\frac{1}{4,8 \text{km/s}}-\frac{1}{8 \text{km/s}}} =360 \text{km}$]]
Aallonpituudet:
[[$ v=\lambda f $]], josta [[$ \lambda=\frac{v}{f} $]]
P-aalto [[$ \lambda=\frac{8\text{km/s}}{2 \ \text{1/s}}=4 \text{km} $]]
S-aalto [[$ \lambda=\frac{4,8\text{km/s}}{10 \ \text{1/s}}=0,48 \text{km} $]]
6.2
P-aalto on pitkittäinen aalto ja S-aalto on poikittainen aalto. Koska eri kiviaineksissa nopeudet ovat kullekin kiviaineelle ominaisia, niin aallon leviämistä tutkimalla saadaan tietoa maapallon kerrosrakenteesta. Aallot myös taittuvat saavuttaessa kahden aineen rajapintaan, joten eri kerroksissa sijaitsevat rajapinnat löydetään tekemällä mittauksia eri kohdissa. Nestemmäisessä osassa liikkuvat vain P-aallot.

7.1 Kun valo osuu kahden aineen rajapintaan, niin osa valosta heijastuu ja osa jatkaa toiseen aineeseen. Seuraavalla rajapinnalla käy samoin. Kun tarkastellaan takaisin tulosuuntaan heijastunutta valoa havaitaan sen inerferoivan yläinnasta heijastuneen valon kanssa. Jos nämä kaksi valansädettä ovat samassa vaiheessa, niin havaitaan valon vahvistuminen. Jos säteet ovat vastakkaisissa vaiheissa ne sammuttavat toisensa. Heijastumisessa tapahtuu lisäksi puolen aallon vaihesiirto, mikäli aalto saapuu optisesti harvemmasta aineesta tiheämpään.

Koska molemmissa
[[$ t_P=\frac{x}{v_P} $]]
Vastaavasti S-aalto
[[$ t_S=\frac{x}{v_S} $]]
Aikaero
[[$ \Delta t=t_S-t_P= \frac{x}{v_S}-\frac{x}{v_P}=x\left(\frac{1}{v_S}-\frac{1}{v_P}\right) $]], josta
[[$ x=\frac{\Delta t}{\frac{1}{v_S}-\frac{1}{v_P}} =\frac{30 \text{s}}{\frac{1}{4,8 \text{km/s}}-\frac{1}{8 \text{km/s}}} =360 \text{km}$]]
Aallonpituudet:
[[$ v=\lambda f $]], josta [[$ \lambda=\frac{v}{f} $]]
P-aalto [[$ \lambda=\frac{8\text{km/s}}{2 \ \text{1/s}}=4 \text{km} $]]
S-aalto [[$ \lambda=\frac{4,8\text{km/s}}{10 \ \text{1/s}}=0,48 \text{km} $]]
6.2
P-aalto on pitkittäinen aalto ja S-aalto on poikittainen aalto. Koska eri kiviaineksissa nopeudet ovat kullekin kiviaineelle ominaisia, niin aallon leviämistä tutkimalla saadaan tietoa maapallon kerrosrakenteesta. Aallot myös taittuvat saavuttaessa kahden aineen rajapintaan, joten eri kerroksissa sijaitsevat rajapinnat löydetään tekemällä mittauksia eri kohdissa. Nestemmäisessä osassa liikkuvat vain P-aallot.

7.1 Kun valo osuu kahden aineen rajapintaan, niin osa valosta heijastuu ja osa jatkaa toiseen aineeseen. Seuraavalla rajapinnalla käy samoin. Kun tarkastellaan takaisin tulosuuntaan heijastunutta valoa havaitaan sen inerferoivan yläinnasta heijastuneen valon kanssa. Jos nämä kaksi valansädettä ovat samassa vaiheessa, niin havaitaan valon vahvistuminen. Jos säteet ovat vastakkaisissa vaiheissa ne sammuttavat toisensa. Heijastumisessa tapahtuu lisäksi puolen aallon vaihesiirto, mikäli aalto saapuu optisesti harvemmasta aineesta tiheämpään.

Koska molemmissa

