REFLECTION AT CURVED SURFACES
REFLECTION AT CURVED SURFACES
Introduction
We have already looked at reflection by plane mirrors in topic 8. When the reflecting surface is instead curved, we call it a curved mirror. There are two types of curved mirrors; concave and convex mirror. Curved mirrors whose reflecting surfaces curve inwards are called concave mirrors while those whose reflecting surfaces bulge outwards are called convex mirrors.
 |
|
Terms
Curved mirrors are parts of a sphere. The following terms are used in curved mirrors:

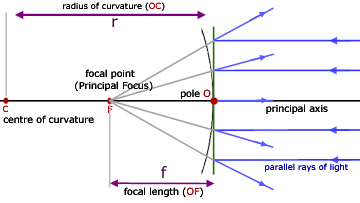
- Pole P- it is the centre of the mirror.
- Centre of curvature C- it is the centre of the sphere of which the mirror is part.
- Radius of curvature r- it is the radius of the sphere of which the mirror is part.
- Principal axis- it is a line drawn through the pole of the mirror and the centre of curvature.
- Principal focus F – for a concave mirror, it is the point at which all rays parallel and close to the principal axis converge at after reflection. In the case of a convex mirror, it is the point at which all rays parallel and close to the principal axis appear to diverge from after reflection.(See the figure above). It is also called the focal point.
- Focal plane- it is a plane perpendicular to the principal axis and passes through the focal point. It is the plane where parallel rays but not parallel to the principal axis converge at or appear to diverge from after reflection.
- Focal length f- it is the distance between the pole of the mirror and its focal point.
When rays are produced behind the mirror, they are indicated using dotted lines. This means that they are imaginary or virtual. Hence the focal point and focal length of a concave mirror are real while the focal point and focal length of a convex mirror arevirtual. A real focal length is given a positive sign while a negative focal length is given a negative sign.
Ray diagrams
Curved mirrors form images when two rays intersect or appear to intersect. In ray diagrams, we use the following symbols to represent the two curved mirrors:

There are four important rays used in ray diagrams. They include:
- A ray passing through C or appearing to pass through C:

The ray is reflected along the same path.
- A ray parallel and close to the principal axis.
The ray is reflected through the principal focus F for a concave mirror or appear to come from the principal focus of the convex mirror.
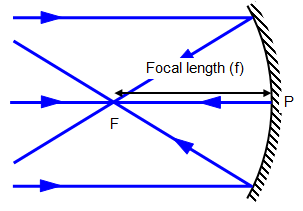
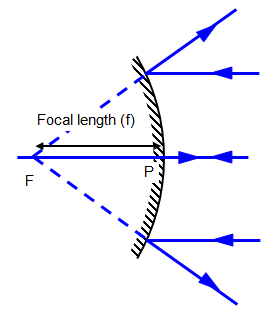
- A ray passing through the principal focus F or appearing to pass through F
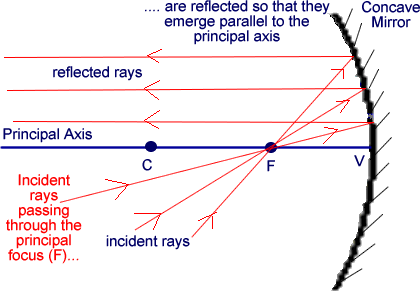
The reflected ray moves parallel to the principal axis (by the principle of reversibility of light).
- A ray incident at the pole of the mirror.

The ray is reflected making the same angle with the principal axis as the incident ray (i.e <i=<r).
Image formation by curved mirrors
The table below provides a summary of how a concave and convex mirror forms images:
|
Position of the object |
Image formation by concave mirror |
Image formation by convex mirror |
|
Object at infinity |
Image formed is inverted, real , diminished and formed at F. |
Image formed is upright, virtual and diminished. |
|
Object beyond C |
Image formed is real, inverted and diminished. |
Image formed is virtual, upright and diminished. |
|
Object at C |
Image formed is real, inverted and same size as the object |
Image formed is virtual, upright and diminished. |
|
Object between C and F |
Image formed is real, inverted and magnified. |
Image formed is virtual, upright and diminished. |
|
Object at F |
Image formed is real, inverted and at infinity. |
Image formed is virtual, upright and diminished. |
|
Object between F and P
|
Image formed is virtual, upright and magnified. |
Image formed is virtual, upright and diminished. |
Note that a concave mirror always forms real and inverted and images except when the object is placed between the focal point and the pole of the mirror when it forms a virtual and inverted image. On the other hand, a convex mirror always forms a virtual, erect and diminished image.
A real image is that image formed by actual intersection of real rays while a virtual image is formed by imaginary rays. Furthermore, a real image can be formed on a screen while a virtual image cannot be formed on a screen.
Linear magnification and the mirror formula
Linear magnification is defined as the ratio of the image size to the object size;
Magnification= Image size/ Object size.
Similarly, it can be expressed as the ratio of the distance of the image to the distance v of object u from the mirror. Magnification has no unit.
Suppose an object is placed u cm in front of a spherical mirror of focal length f such that the image is formed v cm from the mirror, then u, v and f are related by the equation;
1/f= 1/u + 1/v.
This equation is referred to as the mirror formula. The formula holds for both concave and convex mirrors.
When applying the mirror formula, it is necessary to observe the following points:
- That all distances are measured from the mirror as the origin.
- All real distances are positive while all virtual distances are negative.
- A concave mirror has a positive focal length while a convex mirror has a negative focal length.
Example
- Determine the position, size and nature of the image of an object 4cm tall placed on the principal axis of a concave mirror of focal length 15cm at a distance 30cm from the mirror.
solution
u=30cm, f= 15cm, ho=4cm
1/v=1/f-1/u
= 1/15 – 1/30 =1/30
v =30cm
Also, m=v/u =hi/ho
Thus, hi=(30cm x 4cm)/30cm =4cm.
Thus the image formed is real and same size as the object.
2. A convex mirror of focal length 9cm produces an image on its axis 6cm from the mirror. Determine the position of the object.solution
f= -9cm, v= -6cm.
1/u = 1/f – 1/v = -1/9 – (-1/6)
1/u= (-2+3)/ 18 =1/18
u=18cm
Determination of the focal length of a concave mirror
The focal length of a concave mirror can be estimated by focusing a distant object on a screen. Parallel rays from a distant object converge at the focal plane of the mirror.

The distance between the mirror and the screen is the estimated focal length of the concave mirror.
look at the link below.
Alternatively, the object can be placed in front of the concave mirror at various distances and measuring the corresponding image distances then applying the mirror formula. From the values of u and v, appropriate graph is plotted. There are three possible graphs that can be obtained from the mirror formula. These include:
- A graph of 1/v against 1/u
Rearranging the mirror formula, we have;
1/v= -1/u + 1/f
Hence a graph of 1/v against 1/u is a straight line having a negative gradient.
At the y-intercept, 1/u=0. Substituting this in the mirror formula, we obtain;
1/f=1/v. thus the y-intercept is equal to 1/f.
Similarly, at the x-intercept 1/v=0. Substituting in the mirror formula, we obtain;
1/f=1/u i.e the x-intercept is equal to 1/f.
If the values of f obtained from the y-intercept and x-intercept above are different then we determine their average.
- A graph of uv against u+v
From the mirror formula, we have;
1/f=1/u + 1/v =(v+u)/uv
And uv=f(u+v)
Hence a graph of uv against u+v is a straight line through the origin whose slope gives the focal length of the mirror.
uv (cm2)
Slope=f
(u+v) cm
- A graph of magnification M against v
Also from the mirror formula, if we multiply through by v, we obtain:
v/f =v/u + v/v
But v/u =magnification M.
Then, v/f =M+1.
Rearranging the equation we have;
M=v/f -1
Hence a graph of magnification M against v is a straight line whose slope is equal to 1/f and y-intercept is -1.
M
v (cm)
-1
Applications of spherical mirrors and curved reflecting surfaces
Concave mirrors
Concave mirrors are used by dentists to magnify teeth during extraction and as a shaving mirror. In both cases, the mirror forms upright and magnified images. Concave reflectors are also used in projector lamps, solar concentrators and telescopes.
r



shaving mirror
Convex mirrors
Convex mirrors can be used in supermarkets to monitor customers’ activities and as driving mirrors in cars and motorcycles. This is because convex mirrors provide a wide field of view compared to a plane mirror.


However, a convex mirror used as a driving mirror has one limitation. It forms a virtual diminished image which appears to be farther away from the observer than it actually is. This may lead to misjudgment by the observer which can result into accidents.