4.PRESSURE
pressure
Introduction
Pressure is defined as the compressive force acting normally per unit area;
pressure= force/area
The SI unit of pressure is newton per square metre (N/m2). Pressure can also be expressed in pascals (Pa);
1N/m2=1Pa
Atmospheric pressure is sometimes expressed as mmHg, cmHg or atmospheres.
For a given amount of force, the smaller the area of contact the greater the pressure exerted. This explains why it would be easier for a sharp pin to penetrate a piece of cardboard than a blunt one when the same force is used.
A solid resting on a horizontal surface exerts a normal contact force equals to its weight. The pressure of the solid on the surface depends on the area of contact.
The pressure between two solid surfaces depends on two things:
(a) the force between the surfaces
(b) the area of contact between the two surfaces.
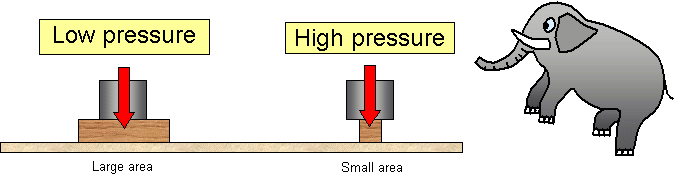
The greater the force or the smaller the area the greater the pressure.
Example
- A man whose mass is 90kg stands on a floor. If the area of contact between his feet and the floor is 0.0368m2,
solutionP= F/A
= 900N/0.0368m2
=24,456.5217N/m2.
b) What pressure will he exert on the floor if now he stands on one foot?
P=900N/(0.0368/2)
=48,913.0435N/m2
Pressure in fluids
A fluid is a term that refers to either liquids and gases. The set up below can be used to illustrate pressure in fluids:
Pressure in fluids increases with depth i.e. the greater the depth the higher the pressure it exerts.
This explains why the walls of a dam are made wider downwards.
A diver under water experiences pressure due to the weight of water above him plus the atmospheric pressure above the water surface. The deeper the diver, the greater the pressure.

When a liquid is poured into a set of connected tubes of different shapes, it rises up until the levels are the same in all the tubes.
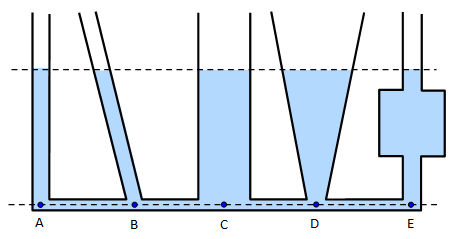
The fluid pressure formula
Consider a liquid of density ρ in a container of uniform cross-section area A, such that the depth of the liquid in the container is h

Volume of the liquid = A*h
Mass = volume * density
=Ahρ
Weight of the liquid = mass * gravitational field intensity= force exerted
=Ahρg
From the definition of pressure, P= F/A
= Ahρg/A
= hρg
It is thus clear that pressure in fluids is directly proportional to the height of the column h, the density of the fluid ρ and the gravitational field strength g.
Note: Pressure in fluids does not depend on the cross section area of the container which holds it.
Example
- Calculate the pressure exerted by a column of kerosene of 0.85m ( take the density of kerosene= 800kgm-3).
P=hρg =0.85m x 800kgm-3x10N/kg
= 6800Pa
Transmission of pressure in fluids
The figure below shows a liquid under pressure due to the force F acting on the plunger.


Assuming that the holes are identical, when the plunger is pushed forward, the liquid squirts out through the holes with equal force. If the piston area is A, then the pressure developed is F/A. this pressure is transmitted equally to all parts of the liquid. This is called Pascal’s principle. The principle states that pressure applied at one part of a liquid is transmitted equally to all other parts of the enclosed liquid. Gases can also transmit pressure in a similar way provided they are incompressible.
see a clip in the link below
The working of hydraulic machines is based on Pascal’s principle.
Atmospheric pressure
The term atmosphere refers to the air surrounding the earth. The weight of air above the earth’s surface exerts pressure on the earth. This pressure is called atmospheric pressure. The presence of atmospheric pressure can be demonstrated by the crushing can experiment;

The can is filled with water then heated for several minutes. After sometime, the can is sealed and then cooled by running cold water over it.
When the water is heated, steam is produced which displaces air in the can. When cold water is run over it, steam condenses leaving a vacuum in the can. Pressure inside is thus reduced below the external atmospheric pressure. Hence the can crushes inwards.
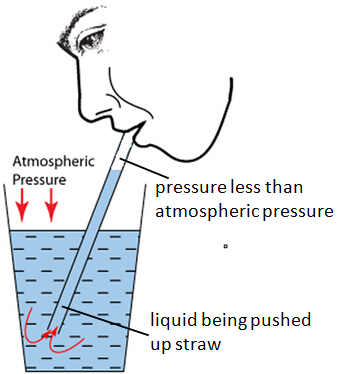
Atmospheric pressure is also very vital when using a drinking straw. By sucking through a drinking straw the pressure inside is reduced. The atmospheric pressure acting on the surface of the liquid overcomes the pressure inside the straw. The pressure difference and hence the resultant force pushes the liquid up the straw.
Measurement of pressure
Atmospheric pressure is measured using an instrument called a barometer. The following are some types of barometers:
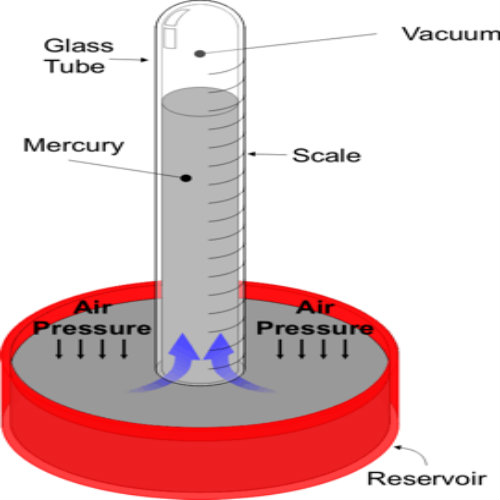
Atmospheric pressure can support a liquid column in a tube. One end of the tube is closed and the tube is filled with mercury. When inverted and with the open end below the liquid surface in the container. The atmospheric pressure (Patm ) on the open surface is transmitted by the liquid to the base of the liquid column and supports its weight.
With the liquid column h, the atmospheric pressure can be determined from the equation;
Pressure = hρg
Where h- is the height of the liquid column
ρ- Density of the liquid (mercury)
g- Gravitational field strength
At sea level atmospheric pressure can support approximately 760mm column of mercury equivalent to approximately 10m column of water. Mercury is thus preferred as a barometric fluid since it gives a shorter and measurable column compared to water.
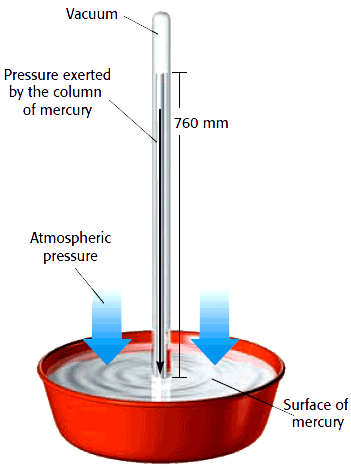

In general, atmospheric pressure decreases with altitude. The value of atmospheric pressure at sea level is called the standard atmospheric pressure and is at times referred to as one atmosphere.
Pressure at sea level =hρg =0.76m*13600kg/m3 *10N/kg
= 103,360N/m2
If there is air trapped in the space above the mercury column then the barometer is faulty. This space above the mercury column is called toricellian vacuum. To test whether this space has some air trapped, the test tube is tilted until it is at the same level with the mercury column when the tube is upright. If the space is truly a vacuum, the test tube will be completely filled with mercury while if it has trapped air a space will still remain at the top.
Normally the toricellian vacuum contains some little mercury vapour.
Note that this barometer is not readily portable.
- A manometer
This is a U-shaped tube open on both ends. One end is connected to a source of gas whose pressure is to be determined. The other arm is open to the atmosphere. This creates a pressure difference which displaces the manometer liquid.

The points 2 and 3 are at the same level and as such experience the same amount of pressure. The pressure at 2 is the gas pressure while that at 3 equals the pressure due to the liquid column plus atmospheric pressure;
Pg = PA + h2ρg
- Fortin barometer
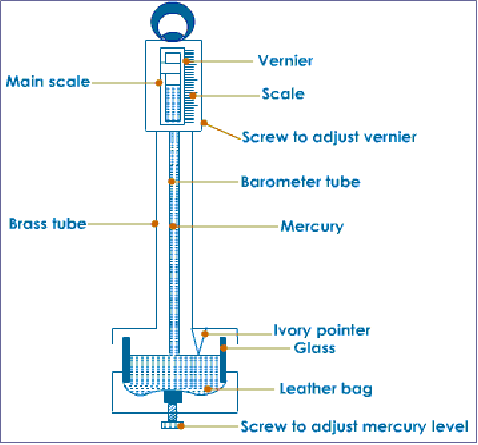 |
|
The fixed ivory index with a sharp point acts asthe zero mark of the main scale. Before taking any reading the level of the mercury in the reservoir must first be adjusted until the tip of the ivory index just touches the surface of mercury.
The height of mercury column is then read from the main scale .this reading is then used to calculate the pressure at the place. Any change in the atmospheric pressure causes the level of mercury in the reservoir to move up or down, hence the adjustment of the ivory index is necessary.
- Aneroid barometer
This type of barometer is more portable.
 |
|
When the pressure outside the vacuum chamberbox is reduced, the box expands setting the levers into motion. However, when the pressure outside increases, the box reduces in volume. The resultant movements of the springs and levers moves the pointer across the scale recording the value of the atmospheric pressure.
The aneroid barometer can also be used to measure heights. For instance, altimeters are aneroid barometers used in aircrafts to measure heights.
- Pressure gauge
Pressure gauges are also easily portable. It is commonly used to measure gas pressure, tyre pressure, etc. It consists of a coiled flexible metal tube. When the pressure inside the tube increases, the tube uncoils. The movement of the tube is magnified by the lever and gear mechanism which then moves the pointer across the scale.
