Mekaaninen työ

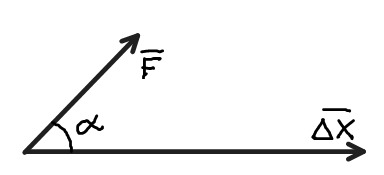
• Voiman F vaikuttaessa kappaleeseen kappaleen samalla liikkuessa, voima F tekee kappaleelle työtä.
• Toisin sanoen voima F syöttää kappaleelle liike-energiaa.
• Välittyvän energian eli työn määrä riippuu voiman ja liikkeen välisestä kulmasta.
• Kun voima F ja kappaleen siirtymä [[$ \Delta x $]]​ ovat samansuuntaiset, työ W on:

​[[$$ W = F \Delta x $$]]​

• Kun voima on siirtymän kanssa vastakkaissuuntainen, voima vähentää liike-energiaa, eli työ on negatiivista:

​[[$$ W = - F \Delta x $$]]​

• Yleisesti ottaen työ voidaan laskea voiman ja liikesuunnan välisen kulma [[$ \alpha $]]​ avulla:

​[[$$ W = F \Delta x \cos (\alpha) $$]]​

• tai vektoreiden pistetulona

​[[$$ W = \bar{F} \cdot \bar{\Delta x}$$]]​

Teho

• Teho P tarkoittaa energian määrää E aikayksikköä t kohden.

[[$$ P = {E \over t} $$]]​

• Energian E paikalla voidaan käyttää myös työn symbolia W tai lämpöenergian symbolia Q.

• Tehon yksikkö on watti W eli toisaalta J/s.

Hyötysuhde

• Hyötysuhdetarkasteluista osa käytettävissä olevasta energiasta muuttuu haluttuun hyödylliseen muotoon ja osa "häviää taivaan tuuliin".
• Hyötyenergian suhdetta kokonaisenergiaan kutsutaan hyötysuhteeksi.
• Koskaan kaikkea energiaa ei saada koskaan muutettua haluttuun muotoon, hyötysuhde on aina pienempi kuin 100 %.
• Hyötysuhde [[$ \eta $]]​ lasketaan yksinkertaisena jakolaskuna:

​[[$$ \eta = {E_{hyöty} \over E_{koko}} $$]]​

• Usein hyötyenergiasta puhutaan antoenergiana ja kokonaisenergiasta ottoenergiana.

​[[$$ \eta = {E_{anto} \over E_{otto} }$$]]​

• Hyötysuhde voidaan laskea myös tehon P avulla, jos tiedetään koneen tai systeemin ottoteho ja antoteho:

​[[$$ \eta = { P_{anto} \over P_{otto}} $$]]​